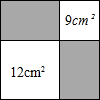
如图.从一个正方形中截取面积为9cm2或12cm2的两个小正方形.则留下阴影部分的面积为12$\sqrt{3}$cm2．题目和参考答案——青夏教育精英家教网—

2．

如图，从一个正方形中截取面积为9cm²或12cm²的两个小正方形，则留下阴影部分的面积为12$\sqrt{3}$cm²．

分析根据图形可得阴影部分的面积等于大正方形面积-两个正方形的面积，然后列式进行计算即可得解．

解答解：因为从一个正方形中截取面积为9cm²或12cm²的两个小正方形，
所以大正方形的边长为：3+2$\sqrt{3}$cm，
所以阴影部分的面积=$（3+2\sqrt{3}）^{2}-9-12=12\sqrt{3}c{m}^{2}$，
故答案为：12$\sqrt{3}$cm²．

点评本题考查算术平方根的问题，根据图形判断出阴影部分的面积等于大正方形面积-两个正方形的面积是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

14．

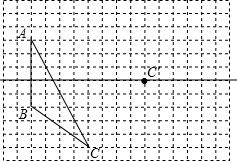画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸中将△ABC经过一次平移后得到△A′B′C′，图中标出了点C的对应点C′．
（1）请画出平移后的△A′B′C′；
（2）若连接AA′，BB′，则这两条线段之间的关系是平行且相等；
（3）利用网格画出△ABC 中AC边上的中线BD；
（4）利用网格画出△ABC 中AB边上的高CE；
（5）△A′B′C′面积为10．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

15．

已知y是关于x的函数，且x，y满足方程组$\left\{\begin{array}{l}{x+3y=4-a}\\{x-y=3a}\end{array}\right.$
（1）求函数y与x的表达式，并在如图所示的坐标系中画出它的图象；
（2）设（1）中的函数与x轴交于点A，过点C（-1，0）作BC⊥x轴交（1）中函数图象于点B，请在x轴上找一点D，连接BD，使得△BCD与△ABC相似（不包括全等），并求出点D的坐标
（3）若点P的坐标为（m，0），求以P为圆心，1为半径的圆与（1）函数的图象有交点时，求m的取值范围
（4）（2）的条件下，如M、N分别是边AB、AD上的动点，连接MN，设AM=DN=n，问是否存在这样的n，使得△AMN与△ADB相似？若存在，请直接写出n的值；若不存在，说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

12．

求作△ABC，使BC=a，AB=c，∠ABC=∠1．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．

把一张边长为40cm的正方形硬纸板，进行适当地裁剪，折成一个长方体盒子（纸板的厚度忽略不计）．
（1）如图，若将正方形硬纸板的四角各剪掉一个同样大小的正方形，剩余部分折成一个无盖的长方体盒子，要使折成的长方体盒子的底面积为484cm²，则剪掉的正方形的边长为多少？
（2）若将正方形硬纸板的四周剪掉一些长方形（即剪掉的长方形至少有一条边在正方形硬纸板的边上），将剩余部分折成一个有盖的长方体盒子，折成的一个长方体盒子的表面积为550cm²，求此时长方体盒子的长、宽、高（只需求出符合要求的一种情况）．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

7．在数3、-2、0、-$\frac{5}{2}$中，最小的数是（　　）

A．

B．

-2

C．

D．

-$\frac{5}{2}$

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

14．5的相反数与-2的差是（　　）