
ЁОЬтФПЁПФГГЌЪаМЦЛЎЙКНјвЛХњМзЁЂввСНжжЭцОпЃЌвбжЊ5МўМзжжЭцОпЕФНјМлгы3МўввжжЭцОпЕФНјМлЕФКЭЮЊ231дЊЃЌ2МўМзжжЭцОпЕФНјМлгы3МўввжжЭцОпЕФНјМлЕФКЭЮЊ141дЊЃЎ
(1)ЧѓУПМўМзжжЁЂввжжЭцОпЕФНјМлЗжБ№ЪЧЖрЩйдЊЃЛ
(2)НќЦкХњЗЂЩЬгагХЛнЛюЖЏЃЌШчЭМЫљЪОЃЌШчЙћГЌЪаОіЖЈдкМзЁЂввСНжжЭцОпжабЁЙКЦфжавЛжжЃЌЧвЪ§СПГЌЙ§20МўЃЌЧыФуАяжњГЌЪаХаЖЯЙКНјФФжжЭцОпИќЪЁЧЎЃЎ

ЁОД№АИЁПЃЈ1ЃЉУПМўМзжжЭцОпЕФНјМлЪЧ30дЊЃЌУПМўввжжЭцОпЕФНјМлЪЧ27дЊЃЛЃЈ2ЃЉМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЩшУПМўМзжжЭцОпЕФНјМлЪЧxдЊЃЌУПМўввжжЭцОпЕФНјМлЪЧyдЊЃЌЗжБ№РћгУ5МўМзжжЭцОпЕФНјМлгы3МўввжжЭцОпЕФНјМлЕФКЭЮЊ231дЊЃЌ2МўМзжжЭцОпЕФНјМлгы3МўввжжЭцОпЕФНјМлЕФКЭЮЊ141дЊЃЌЕУГіЕШЪНЧѓГіД№АИЃЛ
ЃЈ2ЃЉЩшЙКНјЪ§СПЮЊm(mЃО20)МўЃЌдђМзжжЭцОпашвЊ (21mЃЋ180)дЊЃЌввжжЭцОпашвЊ27mдЊЃЎШЛКѓЗжШ§жжЧщПіЬжТлЃКЂйЕБ27m=21m+180ЪБЃЌЂкЕБ27mЃО21m+180ЪБЃЌЂлЕБ27mЃМ21m+180ЪБЃЌЧѓГіД№АИМДПЩЃЎ
ЃЈ1ЃЉЩшУПМўМзжжЭцОпЕФНјМлЪЧxдЊЃЌУПМўввжжЭцОпЕФНјМлЪЧyдЊЃЌгЩЬтвтЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЎ
ЃЎ
Д№ЃКУПМўМзжжЭцОпЕФНјМлЪЧ30дЊЃЌУПМўввжжЭцОпЕФНјМлЪЧ27дЊЃЛ
ЃЈ2ЃЉЩшЙКНјЪ§СПЮЊm(mЃО20)МўЃЌдђМзжжЭцОпашвЊ30ЁС20ЃЋ(mЃ20)ЁС30ЁС0.7=(21mЃЋ180)дЊЃЌввжжЭцОпашвЊ27mдЊЃЎ
ЂйЕБ27m=21m+180ЪБЃЌдђm=30ЃЌЫљвдЕБЙКНјЭцОпе§КУ30МўЃЌбЁдёЙКЦфжавЛжжМДПЩЃЛ
ЂкЕБ27mЃО21m+180ЪБЃЌдђmЃО30ЃЌЫљвдЕБЙКНјЭцОпГЌЙ§30МўЃЌбЁдёЙКМзжжЭцОпЪЁЧЎЃЛ
ЂлЕБ27mЃМ21m+180ЪБЃЌдђmЃМ30ЃЌЫљвдЕБЙКНјЭцОпЩйгк30МўЃЌбЁдёЙКввжжЭцОпЪЁЧЎЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЕЭЬМЛЗБЃЃЌТЬЩЋГіааЁБЕФИХФюЕУЕНЙуДѓШКжкЕФНгЪмЃЌдНРДдНЖрЕФШЫЯВЛЖбЁдёЦяздааГЕзїЮЊГіааЙЄОпЃЎаЁОќКЭАжАжЭЌЪБЦяГЕШЅЭМЪщЙнЃЌАжАжЯШвд150Уз/ЗжЕФЫйЖШЦяаавЛЖЮЪБМфЃЌанЯЂСЫ5ЗжжгЃЌдйвдmУз/ЗжЕФЫйЖШЕНДяЭМЪщЙнЃЎаЁОќЪМжевдЭЌвЛЫйЖШЦяааЃЌСНШЫЦяааЕФТЗГЬЮЊy(Уз)гыЪБМфx(Зжжг)ЕФЙиЯЕШчЭМЃЎЧыНсКЯЭМЯѓЃЌНтД№ЯТСаЮЪЬтЃК
(1)ЬюПеЃКa=________ЃЛb=________ЃЛm=________ЃЎ
(2)ШєаЁОќЕФЫйЖШЪЧ 120 Уз/ЗжЃЌЧѓаЁОќЕкЖўДЮгыАжАжЯргіЪБОрЭМЪщЙнЕФОрРыЃЎ
(3)дк(2)ЕФЬѕМўЯТЃЌАжАжздЕкЖўДЮГіЗЂКѓЃЌЦяаавЛЖЮЪБМфКѓгыаЁОќЯрОр100 УзЃЌДЫЪБ аЁОќЦяааЕФЪБМфЮЊ________ЗжжгЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвУЧЙцЖЈЃК![]() ЃН
ЃН![]() ЃЈaЁй0ЃЉЃЌМДaЕФИКPДЮУнЕШгкaЕФpДЮУнЕФЕЙЪ§ЃЎР§ЃК
ЃЈaЁй0ЃЉЃЌМДaЕФИКPДЮУнЕШгкaЕФpДЮУнЕФЕЙЪ§ЃЎР§ЃК![]() ЃН
ЃН![]()
ЃЈ1ЃЉМЦЫуЃК![]() ЃН__ЃЛ
ЃН__ЃЛ![]() ЃН__ЃЛ
ЃН__ЃЛ
ЃЈ2ЃЉШчЙћ![]() ЃН
ЃН![]() ЃЌФЧУДpЃН__ЃЛШчЙћ
ЃЌФЧУДpЃН__ЃЛШчЙћ![]() ЃН
ЃН![]() ЃЌФЧУДaЃН__ЃЛ
ЃЌФЧУДaЃН__ЃЛ
ЃЈ3ЃЉШчЙћ![]() ЃН
ЃН![]() ЃЌЧвaЁЂpЮЊећЪ§ЃЌЧѓТњзуЬѕМўЕФaЁЂpЕФШЁжЕЃЎ
ЃЌЧвaЁЂpЮЊећЪ§ЃЌЧѓТњзуЬѕМўЕФaЁЂpЕФШЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСРэНт
Ёп![]() ЃМ
ЃМ![]() ЃМ
ЃМ![]() ЃЌМД2ЃМ
ЃЌМД2ЃМ![]() ЃМ3ЃЎ
ЃМ3ЃЎ
Ёр![]() ЕФећЪ§ВПЗжЮЊ2ЃЌаЁЪ§ВПЗжЮЊ
ЕФећЪ§ВПЗжЮЊ2ЃЌаЁЪ§ВПЗжЮЊ![]() Љ2ЃЌ
Љ2ЃЌ
Ёр1ЃМ![]() Љ1ЃМ2
Љ1ЃМ2
Ёр![]() Љ1ЕФећЪ§ВПЗжЮЊ1ЃЎ
Љ1ЕФећЪ§ВПЗжЮЊ1ЃЎ
Ёр![]() Љ1ЕФаЁЪ§ВПЗжЮЊ
Љ1ЕФаЁЪ§ВПЗжЮЊ![]() Љ2
Љ2
НтОіЮЪЬтЃКвбжЊЃКaЪЧ![]() Љ3ЕФећЪ§ВПЗжЃЌbЪЧ
Љ3ЕФећЪ§ВПЗжЃЌbЪЧ![]() Љ3ЕФаЁЪ§ВПЗжЃЌ
Љ3ЕФаЁЪ§ВПЗжЃЌ
ЧѓЃКЃЈ1ЃЉaЃЌbЕФжЕЃЛ
ЃЈ2ЃЉЃЈЉaЃЉ3+ЃЈb+4ЃЉ2ЕФЦНЗНИљЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћвЛдЊвЛДЮЗНГЬЕФИљЪЧвЛдЊвЛДЮВЛЕШЪНзщЕФНтЃЌдђГЦИУвЛдЊвЛДЮЗНГЬЮЊИУВЛЕШЪНзщЕФЙиСЊЗНГЬЃЎ
ЃЈ1ЃЉдкЗНГЬЂй3xЃ1=0ЃЌЂк ![]() ЂлxЃ(3x+1)=Ѓ5 жаЃЌВЛЕШзщ
ЂлxЃ(3x+1)=Ѓ5 жаЃЌВЛЕШзщ![]() ЕФЙиСЊЗНГЬЪЧ________
ЕФЙиСЊЗНГЬЪЧ________
ЃЈ2ЃЉШєВЛЕШЪНзщ 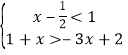 ЕФвЛИіЙиСЊЗНГЬЕФИљЪЧећЪ§ЃЌ дђетИіЙиСЊЗНГЬПЩвдЪЧ________ЃЈаДГівЛИіМДПЩЃЉ
ЕФвЛИіЙиСЊЗНГЬЕФИљЪЧећЪ§ЃЌ дђетИіЙиСЊЗНГЬПЩвдЪЧ________ЃЈаДГівЛИіМДПЩЃЉ
ЃЈ3ЃЉШєЗНГЬ 3Ѓx=2xЃЌ3+x= ![]() ЖМЪЧЙигк x ЕФВЛЕШЪНзщ
ЖМЪЧЙигк x ЕФВЛЕШЪНзщ ![]() ЕФЙиСЊЗНГЬЃЌжБНгаДГі m ЕФШЁжЕЗЖЮЇ.
ЕФЙиСЊЗНГЬЃЌжБНгаДГі m ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГПЦММЙЋЫОбаЗЂГівЛПюЖраЭКХЕФжЧФмЪжБэЃЌвЛМвДњРэЩЬГіЪлИУЙЋЫОЕФAаЭжЧФмЪжБэШЅФъЯњЪлзмЖюЮЊ80000дЊ,НёФъAаЭжЧФмЪжБэЕФЪлМлУПжЛБШШЅФъНЕЕЭСЫ600дЊЃЌШєЪлГіЕФЪ§СПгыШЅФъЯрЭЌЃЌЯњЪлзмЖюНЋБШШЅФъМѕЩйСЫ25%.
ЃЈ1ЃЉЧыЮЪНёФъAаЭжЧФмЪжБэУПжЛЪлМлЖрЩйдЊЃП
ЃЈ2ЃЉНёФъетМвДњРэЩЬзМБИаТНјвЛХњAаЭжЧФмЪжБэКЭBаЭжЧФмЪжБэЙВ100жЛЃЌЫќУЧЕФНјЛѕМлИёгыЯњЪлМлИёШчБэ.ШєBаЭжЧФмЪжБэНјЛѕСПВЛГЌЙ§AаЭжЧФмЪжБэЪ§СПЕФ3БЖЃЌЫљНјжЧФмЪжБэПЩШЋВПЪлЭъЃЌЧыФуЩшМЦГіНјЛѕЗНАИЃЌЪЙетХњжЧФмЪжБэЛёРћзюЖрЃЌВЂЧѓГізюДѓРћШѓЪЧЖрЩйдЊЃП
AаЭжЧФмЪжБэ | BаЭжЧФмЪжБэ | |
НјМл | 1300дЊ/жЛ | 1500дЊ/жЛ |
ЪлМл | НёФъЕФЪлМл | 2300дЊ/жЛ |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКEЪЧЁЯAOBЕФЦНЗжЯпЩЯвЛЕуЃЌECЁЭOBЃЌEDЁЭOAЃЌCЁЂDЪЧДЙзуЃЌСЌНгCDЃЌНЛOEгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКOD=OCЃЛ
ЃЈ2ЃЉШєЁЯAOB=60ЁуЃЌЧѓжЄЃКOE=4EFЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
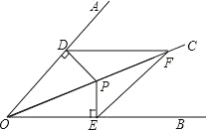
ЁОЬтФПЁПШчЭМЃЌ OC ЪЧAOB ЕФЦНЗжЯпЃЌ P ЪЧOC ЩЯЕФвЛЕуЃЌ PD OA гк D ЃЌPE OB гк E ЃЎ F ЪЧOC ЩЯЕФСэвЛЕуЃЌСЌНг DF ЁЂ EF ЃЎ
ЃЈ1ЃЉЧѓжЄЃК DPF EPF ЃЛ
ЃЈ2ЃЉБШНЯ DF гы EF ЕФДѓаЁЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com