
【题目】如图,点B(3,3)在双曲线![]() (x>0)上,点D在双曲线
(x>0)上,点D在双曲线![]() (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(1)求k的值;
(3)求点A的坐标.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧BC的中点,点D是优弧BC上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=6![]() cm;③sin∠AOB=
cm;③sin∠AOB=![]() ;④四边形ABOC是菱形.其中正确结论的序号是( )
;④四边形ABOC是菱形.其中正确结论的序号是( )

A. ①③ B. ①②③④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°.

(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙两个空调安装队分别为A、B两个公司安装空调,甲安装队为A公司安装66台空调,乙安装队为B公司安装80台空调,乙安装队提前一天开工,最后与甲安装队恰好同时完成安装任务.已知甲队比乙队平均每天多安装2台空调,求甲、乙两个安装队平均每天各安装多少台空调.
查看答案和解析>>
科目:初中数学 来源: 题型:
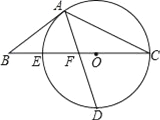
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2+kx﹣3=0的一个根是x=1,则另一个根是___.
【答案】-3.
【解析】
解:∵x=1是一元二次方程的根,∴12+k×1-3=0,∴k=2,∴x2+2x-3=0,∴(x+3)(x-1)=0,∴x1=-3,x2=1.故答案为:-3.
【题型】填空题
【结束】
19
【题目】如图,在△ABC中,AB=8,AC=6,AD=12,点D在BC的延长线上,且△ACD∽△BAD,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com