
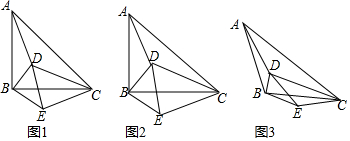
分析 (1)先判断出△ABC∽△DEC,得出$\frac{BC}{CE}=\frac{AC}{CD}$,即可得出结论;
(2)先求出AC=$\sqrt{{n}^{2}+1}$BC,同理:CD=$\sqrt{{n}^{2}+1}$EC,再判断出△ABC∽△DEC,得出比例式,继而判断出△ACD∽△BCE,即可得出AD=$\sqrt{{n}^{2}+1}$BE,BE=$\frac{2}{\sqrt{{n}^{2}+1}}$,再利用勾股定理得出DE2=$\frac{9{n}^{2}}{{n}^{2}+1}$再判断出∠DBE=90°,再用勾股定理得出DE的平方,用DE的平方建立方程求解即可;
(3)同(2)的方法$\frac{c}{CE}=\frac{b}{BE}$,再构造直角三角形,利用勾股定理即可得出结论.
解答 解:(1)∵△ABC与△DEC均为等腰直角三角形,且∠ABC=∠DEC=90°,
∴△ABC∽△DEC,
∴$\frac{BC}{CE}=\frac{AC}{CD}$,∠ACB=∠DCE,
∴∠ACD=∠BCE,
∵$\frac{BC}{CE}=\frac{AC}{CD}$,
∴△ACD∽△BCE;
(2)在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{n}^{2}+1}$BC,
同理:CD=$\sqrt{{n}^{2}+1}$EC,
∵∠ABC=∠DEC=90°,
∵$\frac{AB}{BC}$=$\frac{DE}{EC}$,
∴$\frac{AB}{DE}=\frac{BC}{CE}$
∴△ABC∽△DEC,
∴$\frac{BC}{CE}=\frac{AC}{CD}$=$\frac{AB}{DE}$,∠ACB=∠DCE,
∴∠ACD=∠BCE,
∵$\frac{BC}{CE}=\frac{AC}{CD}$,
∴△ACD∽△BCE,
∴$\frac{AC}{BC}=\frac{CD}{CE}=\frac{AD}{BE}$=$\sqrt{{n}^{2}+1}$,
∴AD=$\sqrt{{n}^{2}+1}$BE,
∵AD=2,
∴BE=$\frac{2}{\sqrt{{n}^{2}+1}}$,
在Rt△CDE中,CD2=DE2+CE2=(n2+1)CE2=9,
∴CE2=$\frac{9}{{n}^{2}+1}$
∴DE2=n2CE2=n2×$\frac{9}{{n}^{2}+1}$=$\frac{9{n}^{2}}{{n}^{2}+1}$,
∵△ACD∽△BCE,
∴∠CAD=∠CBE,∵∠CAD+∠CBD=90°,
∴∠DBE=∠CBE+∠CBE=90°,
在Rt△BDE中,DE2=BD2+BE2=1+$\frac{4}{{n}^{2}+1}$,
∴$\frac{9{n}^{2}}{{n}^{2}+1}$=1+$\frac{4}{{n}^{2}+1}$,
∴n=-$\frac{\sqrt{10}}{4}$(舍)或n=$\frac{\sqrt{10}}{4}$;
(3)c2-b2=(2+$\sqrt{2}$)a2,
理由:如图, ∵AB=BC,DE=EC,
∵AB=BC,DE=EC,
∴$\frac{AB}{DE}=\frac{BC}{CE}$,
∵∠ABC=∠DEC,
∴△ABC∽△DEC,
∴$\frac{BC}{EC}=\frac{AC}{CD}$,
∵AB=BC,DE=EC,且∠ABC=∠DEC=135°,
∴∠ACB=∠DCE=22.5°,
∴∠ACD=∠BCE,
∵$\frac{BC}{EC}=\frac{AC}{CD}$,
∴△ACD∽△BCE,
∴$\frac{AC}{BC}=\frac{CD}{CE}=\frac{AD}{BE}$,
∴$\frac{c}{CE}=\frac{b}{BE}$,
过点D作DF⊥CE交CE的延长线于F,
∵∠DEC=135°,
∴∠DEF=45°,
设DF=x,
∴EF=x,DE=$\sqrt{2}$x,
∵EC=DE=$\sqrt{2}$x,
∴CF=EF+EC=($\sqrt{2}$+1)x,
在Rt△CDF中,CF2+DF2=CD2,
∴[($\sqrt{2}$+1)x]2+x2=c2,
∴x2=$\frac{{c}^{2}}{4+2\sqrt{2}}$,
∴DE2=2x2=$\frac{{c}^{2}}{2+\sqrt{2}}$,
∴BE2=$\frac{{b}^{2}C{E}^{2}}{{c}^{2}}$=$\frac{{b}^{2}}{{c}^{2}}$×$\frac{{c}^{2}}{2+\sqrt{2}}$=$\frac{{b}^{2}}{2+\sqrt{2}}$,
∵△ACD∽△BCE,
∴∠CAD=∠CBE,
∵∠CAD+∠CBD=90°,
∴∠DBE=∠CBE+∠CBE=90°,
在Rt△BDE中,DE2=BD2+BE2,
∴$\frac{{c}^{2}}{2+\sqrt{2}}$=a2+$\frac{{b}^{2}}{2+\sqrt{2}}$,
∴c2-b2=(2+$\sqrt{2}$)a2.
点评 此题是相似形综合题,主要考查了等腰直角三角形的性质,相似三角形的判定和性质,勾股定理,直角三角形的判定,解本题的关键是得出∠DBE=90°和利用两边对应成比例夹角相等来判断两三角形相似的方法应用,还用到类比的方法解决问题.


科目:初中数学 来源:2017届辽宁省九年级3月月考数学试卷(解析版) 题型:填空题
在一个不透明的口袋中装有若干个只有颜色不同的球,如果已知袋中只有3个红球,且一次摸出一个球是红球的概率为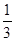 ,那么袋中的球共有 个.
,那么袋中的球共有 个.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
估算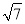 的值是( )
的值是( )
A. 在1和2之间 B. 在2和3之间
C. 在3和4之间 D. 在4和5之间
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
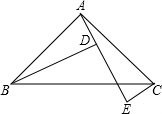 如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.
如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com