
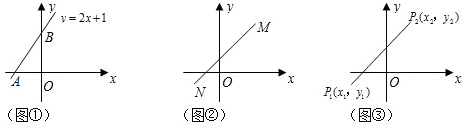
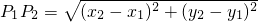 .
. (1)解:由y=0,得x=-2,所以点A的坐标为(-2,0),故OA=2.
(1)解:由y=0,得x=-2,所以点A的坐标为(-2,0),故OA=2.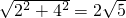 ;
;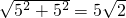 ;
;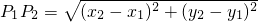 .(10分
.(10分

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
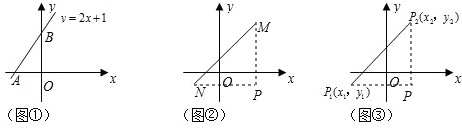
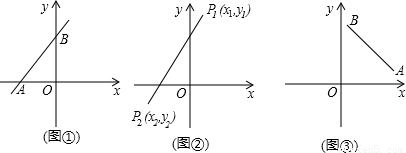
| (x2-x1)2+(y2-y1)2 |
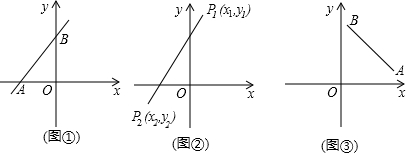
查看答案和解析>>
科目:初中数学 来源: 题型:044
先阅读,后解答下列题目:
甲数比乙数的一半少2,已知甲数等于3,求乙数.
解:设 乙数为x,根据题意,得![]() ,x=10.
,x=10.
象上面解题的思想方法,我们称之为方程思想,请用列方程的方法解答下题:
某学校七(5)班一部分同学进行个人投篮比赛,受污损的下表记录了在规定时间内投进n个球的人数分布情况:
|
进球数n |
0 |
1 |
2 |
3 |
4 |
5 |
|
投进n个球的人数 |
1 |
2 |
7 |
2 |
(1)同时,已知进3个球的人数是进4个球人数的3倍,并且进球3个或3个以上的人平均投进3.5个球,问投进3个球与4个球的人各有多少人?
(2
)根据题目,仿照(1),编一道应用题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
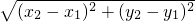 ;
;
查看答案和解析>>
科目:初中数学 来源:2010年福建省莆田市中考数学仿真模拟试卷(三)(解析版) 题型:解答题
 ;
;
查看答案和解析>>
科目:初中数学 来源:模拟题 题型:解答题
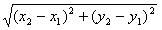
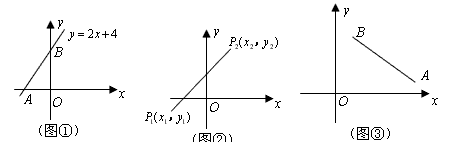
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com