
����Ŀ���ɶ���Ϊ����ʵ�ƽ�����ƶ��������̨���������ס�ҽ����ƶ��������������ҵ���֡������йܺ��ذ�Ǩ�����ְ����ʩ��ÿ��ƶ������������2��5�ְ����ʩ���ְ�������2�֡�3�֡�4�ֺ�5�ְ����ʩ��ƶ�����ֱ��ΪA��B��C��D��ƶ������Ϊ�������ʩ�Ƿ���ʵ�������ȡ������ƶ�������е��飬�ֽ��ռ������ݻ��Ƴ���ͼ������������ͳ��ͼ�������ͼ����Ϣ���ش��������⣺
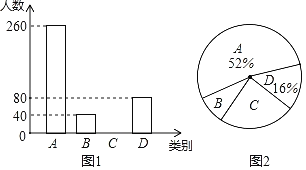
��1�����γ��������˶��ٻ�ƶ������
��2���ɶ��й���9100��ƶ��������������ٵõ�4�ְ����ʩ�Ĵ�Լ�ж��ٻ���
��3��2020���Ǿ���ƶ�����꣬Ϊ���õ����ù�����������D��ƶ�����еļס��ҡ��������Ļ������ѡȡ���������Ե�����������״ͼ���б������ǡ��ѡ���Һͱ��ĸ��ʣ�
���𰸡���1��500������2��3640������3����״ͼ��������![]()
��������
��1����A������������Ӧ�ٷֱȿɵô𰸣�
��2�����ٵõ�4�ְ����ʩ��C��D������������C��D��Ӧ�ٷֱȵĺͣ����ɵõ��𰸣�
��3������״ͼ���б������еȿ��ܵĽ���оٳ��������ø��ʹ�ʽ��⼴�ɣ�
�⣺��1�����γ���������ܻ���Ϊ260��52%��500��������
��2�����B��ƶ������ռ���γ���������ܻ����İٷ���Ϊ��![]() ��100%��8%��
��100%��8%��
���C��ƶ������ռ���γ���������ܻ����İٷ���Ϊ��1��52%��16%��8%��24%��
�������ٵõ�4������ʩ�Ĵ�Լ��9100����24%+16%����3640��������
��3������״ͼ���£�
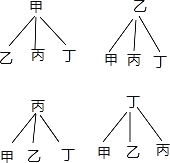
����״ͼ֪����12�ֿ��ܽ��������ǡ��ѡ���Һͱ�����2�ֽ����
����ǡ��ѡ���Һͱ��ĸ���Ϊ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
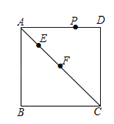
����Ŀ����ͼ����������![]() �У�
��![]() ��
��![]() ��
��![]() �ǶԽ���
�ǶԽ���![]() �ϵ���������(��
�ϵ���������(��![]() ������
������![]() )����
)����![]() ��
��![]() ���������ı��ϵ�����һ�㣮��
���������ı��ϵ�����һ�㣮��![]() �ǵȱ������Σ��� AE�ij�Ϊ______ ��
�ǵȱ������Σ��� AE�ij�Ϊ______ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
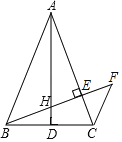
����Ŀ����ͼ������ABC�У�AB��AC��AD�DZ�BC�ϵ����ߣ�BE��AC�ڵ�E����AD�ڵ�H����C��CF��AB��BE���ӳ����ڵ�F��
��1����֤����ABH�ס�BFC��
��2����֤��BH2��HEHF��
��3����AB��2����BAC��45������BH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�������Թ��д���ȫ����������֪ʶ���������һ�꼶ȫ��ͬѧ�μ���֪ʶ������
�ռ��̾ݣ��������ȡ�˳�һ�꼶![]() ��ͬѧ��������֪ʶ�������ɼ����������£���λ���֣���
��ͬѧ��������֪ʶ�������ɼ����������£���λ���֣���
�����������ݣ�
�ɼ� | Ƶ���������� |
|
|
|
|
|
|
|
|
��1���뽫ͼ���п�ȱ�IJ��ֲ���������
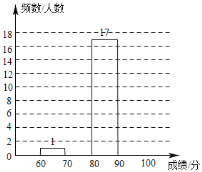
��2��ѧУ��������������֪ʶ�������ɼ���![]() �ּ������ϵ�ͬѧ����������ͳ�ƽ�����Ƹ�У��һ�꼶
�ּ������ϵ�ͬѧ����������ͳ�ƽ�����Ƹ�У��һ�꼶![]() ���У�Լ�ж����˽���ñ��ã�
���У�Լ�ж����˽���ñ��ã�
��3��������֪ʶ�������У��ܵ����õ�С��ͬѧ�õ���ӡ�й��ȡ���ֽ���ʵơ�����ͼ������ö�����£�������ѡȡ��ö���ܵܣ���С�����ܵܵ���ö�������У�ǡ���п���ͼ���ĸ�����______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
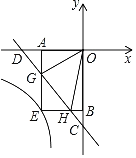
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y����x��2��x�ᣬy��ֱ��ڵ�D��C����G��H���߶�CD�ϵ��������㣬�ҡ�GOH��45��������G��GA��x����A������H��HB��y����B���ӳ�AG��BH���ڵ�E�������E�ķ���������y��![]() �Ľ���ʽΪ_____��
�Ľ���ʽΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и�ѧУ������Ӧ�ϼ���ͣ�β�ͣ�̡��β�ͣѧ����Ҫ��չ�˿������߽�ѧ.��У��������ֱ������������Ƚ�������������ʾ����ڣ����ڽ����Ϊ����: A.�dz����⣻B.�����⣻C.һ�㣻D.�����⣬���ռ�������Ϣ������ͳ�ƣ����Ƴ����²�������ͳ�Ʊ���ͳ��ͼ(��ͼ��ʾ).�������ͳ��ͼ�����ṩ����Ϣ�����������:
��1�������ʾ������ѧ������__ _�ˣ�![]() ��
��![]() ��
��
��2����ȫ����ͳ��ͼ��
Ƶ���ֲ�ͳ�Ʊ�
��� | Ƶ�� | Ƶ�� |
|
|
|
|
|
|
|
|
|
|
|
|
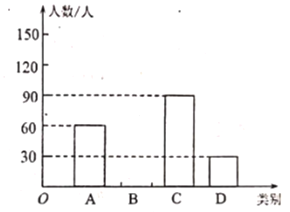
��3������У����ѧ��![]() �ˣ�����������������������Ƹ�У��������ֱ�����������Ϊ
�ˣ�����������������������Ƹ�У��������ֱ�����������Ϊ![]() ���
���![]() ���ѧ�����ж����ˣ�
���ѧ�����ж����ˣ�
��4��Ϊ�Ľ���ѧ��ѧУ������ѡ������![]() ���ѧ���У�ѡȡ�ס��ҡ����������ˣ������ȡ����ͬѧ����������̸�ᣬ��ס�������ͬѧͬʱ�����еĸ��ʣ�
���ѧ���У�ѡȡ�ס��ҡ����������ˣ������ȡ����ͬѧ����������̸�ᣬ��ס�������ͬѧͬʱ�����еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
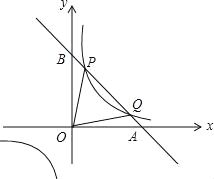
����Ŀ����ֱ֪��y=kx+b��x�ᡢy��ֱ���A��B���㣬�뷴������������һ�����ڵ�P��![]() ��n����Q��4��m�����㣬��tan��BOP=
��n����Q��4��m�����㣬��tan��BOP=![]() ��
��
��1������������ֱ�ߵĺ�������ʽ��
��2������OPQ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC����B=90�㣬BC=6��AD=3��AB=![]() ����E��Fͬʱ��B�������������BC���������ƶ�����֪��F���ƶ��ٶ��ǵ�E�ƶ��ٶȵ�2������EFΪһ����CB���Ϸ����ȱߡ�EFG����E���ƶ�����Ϊx��0��x��6����
����E��Fͬʱ��B�������������BC���������ƶ�����֪��F���ƶ��ٶ��ǵ�E�ƶ��ٶȵ�2������EFΪһ����CB���Ϸ����ȱߡ�EFG����E���ƶ�����Ϊx��0��x��6����
��1����DCB=�� ���ȣ�����G���ı���ABCD�ı���ʱ��x=�� ����
��2���ڵ�E��F���ƶ������У���Gʼ����BD��BD���ӳ������˶������G���߶�BD���е�ʱx��ֵ��
��3����2��x��6ʱ�����EFG���ı���ABCD�ص��������y��x֮��ĺ�����ϵʽ����xȡ��ֵʱ��y�����ֵ�������y�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У������²�����ͼ���ٷֱ��Ե�C�͵�DΪԲ�ģ�����![]() Ϊ�뾶�������������ڵ�M��N������ֱ��MN����
Ϊ�뾶�������������ڵ�M��N������ֱ��MN����![]() ǡ�þ�����A����CD���ڵ�E������BE��������˵��������ǣ� ��
ǡ�þ�����A����CD���ڵ�E������BE��������˵��������ǣ� ��
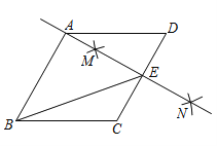
A.![]() B.
B.![]() C.��AB=4����
C.��AB=4����![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com