
【题目】让我们轻松一下,做一个数字游戏.第一步:取一个自然数![]() ,计算
,计算![]() 得
得![]() ;第二步:算出
;第二步:算出![]() 的各位数字之和得
的各位数字之和得![]() ,计算
,计算![]() 得
得![]() ;第三步:算出
;第三步:算出![]() 的各位数字之和得
的各位数字之和得![]() ,计算
,计算![]() 得
得![]() ;
;![]() 依此类推,则
依此类推,则![]() 的值为
的值为![]()
![]()
A.26B.65C.122D.123
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后
的纪录如下:回答下列问题:

(1)这8筐白菜中最接近标准重量的这筐白菜重 千克;
(2)若这批白菜以2元 ∕ 千克的价格出售,则这批白菜一共可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2﹣2x+c(a≠0)与x轴、y轴分别交于点A,B,C三点,已知点A(﹣2,0),点C(0,﹣8),点D是抛物线的顶点.
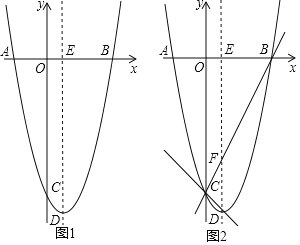
(1)求抛物线的解析式及顶点D的坐标;
(2)如图1,抛物线的对称轴与x轴交于点E,第四象限的抛物线上有一点P,将△EBP沿直线EP折叠,使点B的对应点B'落在抛物线的对称轴上,求点P的坐标;
(3)如图2,设BC交抛物线的对称轴于点F,作直线CD,点M是直线CD上的动点,点N是平面内一点,当以点B,F,M,N为顶点的四边形是菱形时,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) (-3)+(-8)-(-6)-7;
(2)-30×(![]() -
-![]() +
+![]() );
);
(3) (![]() -
-![]() )÷(-
)÷(-![]() )2-23;
)2-23;
(4)-42÷![]() -0.25×[5-(-3)2].
-0.25×[5-(-3)2].
查看答案和解析>>
科目:初中数学 来源: 题型:
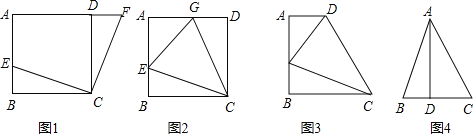
【题目】(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下列两题:
①如图3,在四边形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=12,E是AB上一点,且∠DCE=45°,BE=4,则DE= .
②如图4,在△ABC中,∠BAC=45°,AD⊥BC,且BD=2,AD=6,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
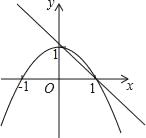
【题目】如图,已知抛物线y1=﹣x2+1,直线y2=﹣x+1,当x任取一值时,x对应的函数值分别为y1,y2.若y1≠y2,取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=2时,y1=﹣3,y2=﹣1,y1<y2,此时M=﹣3.下列判断中:
①当x<0或x>1时,y1<y2;
②当x<0时,M=y1;
③使得M=![]() 的x的值是﹣
的x的值是﹣![]() 或
或![]() ;
;
④对任意x的值,式子![]() =1﹣M总成立.
=1﹣M总成立.
其中正确的是_____(填上所有正确的结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
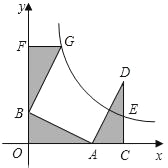
【题目】如图,在平面直角坐标系中,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=![]() ,反比例函数y=
,反比例函数y=![]() (k>0)的图象过CD的中点E.
(k>0)的图象过CD的中点E.
(1)求k的值;
(2)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,试判断点G是否在反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
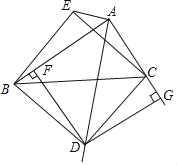
【题目】如图,含45°角的直角三角板DBC的直角顶点D在∠BAC的角平分线AD上,DF⊥AB于F,DG⊥AC于G,将△DBC沿BC翻转,D的对应点落在E点处,当∠BAC=90°,AB=4,AC=3时,△ACE的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com