
”¾ĢāÄæ”æ¹ā»ŖÅ©»ś×āĮŽ¹«Ė¾¹²ÓŠ50ĢØĮŖŗĻŹÕøī»ś£¬ĘäÖŠ¼×ŠĶ20ĢØ£¬ŅŅŠĶ30ĢØ£¬ĻČ½«Õā50ĢØĮŖŗĻŹÕøī»śÅÉĶłA”¢BĮ½µŲĒųŹÕøīŠ”Āó£¬ĘäÖŠ30ĢØÅÉĶłAµŲĒų£¬20ĢØÅÉĶłBµŲĒų£®Į½µŲĒųÓėøĆÅ©»ś×āĮŽ¹«Ė¾ÉĢ¶ØµÄĆæĢģµÄ×āĮŽ¼Ūøń¼ū±ķ£ŗ
ĆæĢؼ׊ĶŹÕøī»śµÄ×ā½š | ĆæĢØŅŅŠĶŹÕøī»śµÄ×ā½š | |
AµŲĒų | 1800 | 1600 |
BµŲĒų | 1600 | 1200 |
£Ø1£©ÉčÅÉĶłAµŲĒųxĢØŅŅŠĶĮŖŗĻŹÕøī»ś£¬×āĮŽ¹«Ė¾Õā50ĢØĮŖŗĻŹÕøī»śŅ»Ģģ»ńµĆµÄ×ā½šĪŖy£ØŌŖ£©£¬ĒóyÓėx¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Š“³öxµÄȔֵ·¶Ī§£»
£Ø2£©ČōŹ¹Å©»ś×āĮŽ¹«Ė¾Õā50ĢØĮŖŗĻŹÕøī»śŅ»Ģģ»ńµĆµÄ×ā½š×ܶī²»µĶÓŚ79 600ŌŖ£¬ĖµĆ÷ÓŠ¶ąÉŁÖÖ·ÖÅä·½°ø£¬²¢½«ø÷ÖÖ·½°øÉč¼Ę³öĄ“£»
£Ø3£©Čē¹ūŅŖŹ¹Õā50ĢØĮŖŗĻŹÕøī»śĆæĢģ»ńµĆµÄ×ā½š×īøߣ¬ĒėÄćĪŖ¹ā»ŖÅ©»ś×āĮŽ¹«Ė¾ĢįŅ»ĢõŗĻĄķ»Æ½ØŅ飮
”¾“š°ø”æ
”¾1”æ 
”¾2”æ 
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāŗĶ±ķøńÖŠµÄŹż¾ŻæÉŅŌµĆµ½y¹ŲÓŚxµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©øł¾ŻĢāŅāæÉŅŌµĆµ½ĻąÓ¦µÄ²»µČŹ½£¬“Ó¶ųæÉŅŌ½ā“š±¾Ģā£»
£Ø3£©øł¾Ż£Ø1£©ÖŠµÄŗÆŹż½āĪöŹ½ŗĶŅ»“ĪŗÆŹżµÄŠŌÖŹæÉŅŌ½ā“š±¾Ģā£®
½ā£ŗ£Ø1£©ÉčÅÉĶłAµŲĒųxĢØŅŅŠĶĮŖŗĻŹÕøī»ś£¬ŌņÅÉĶłBµŲĒųxĢØŅŅŠĶĮŖŗĻŹÕøī»śĪŖ£Ø30©x£©ĢØ£¬ÅÉĶłA”¢BµŲĒųµÄ¼×ŠĶĮŖŗĻŹÕøī»ś·Ö±šĪŖ£Ø30©x£©ĢØŗĶ£Øx©10£©ĢØ£¬
”ąy=1600x+1200£Ø30©x£©+1800£Ø30©x£©+1600£Øx©10£©=200x+74000£Ø10”Üx”Ü30£©£»
£Ø2£©ÓÉĢāŅāæÉµĆ£¬
200x+74000”Ż79600£¬µĆx”Ż28£¬
”ą28”Üx”Ü30£¬xĪŖÕūŹż£¬
”ąx=28”¢29”¢30£¬
”ąÓŠČżÖÖ·ÖÅä·½°ø£¬
·½°øŅ»£ŗÅÉĶłAµŲĒųµÄ¼×ŠĶĮŖŗĻŹÕøī»ś2ĢØ£¬ŅŅŠĶĮŖŗĻŹÕøī»ś28ĢØ£¬ĘäÓąµÄČ«ÅÉĶłBµŲĒų£»
·½°ø¶ž£ŗÅÉĶłAµŲĒųµÄ¼×ŠĶĮŖŗĻŹÕøī»ś1ĢØ£¬ŅŅŠĶĮŖŗĻŹÕøī»ś29ĢØ£¬ĘäÓąµÄČ«ÅÉĶłBµŲĒų£»
·½°øČż£ŗÅÉĶłAµŲĒųµÄ¼×ŠĶĮŖŗĻŹÕøī»ś0ĢØ£¬ŅŅŠĶĮŖŗĻŹÕøī»ś30ĢØ£¬ĘäÓąµÄČ«ÅÉĶłBµŲĒų£»
£Ø3£©ÅÉĶłAµŲĒų30ĢØŅŅŠĶĮŖŗĻŹÕøī»ś£¬20Ģؼ׊ĶĮŖŗĻŹÕøī»śČ«²æÅÉĶłBµŲĒų£¬Ź¹øĆ¹«Ė¾50ĢØŹÕøī»śĆæĢģ»ńµĆ×ā½š×īøߣ¬
ĄķÓÉ£ŗ”ßy=200x+74000ÖŠyĖęxµÄŌö“ó¶ųŌö“ó£¬
”ąµ±x=30Ź±£¬yČ”µĆ×ī“óÖµ£¬“ĖŹ±y=80000£¬
”ąÅÉĶłAµŲĒų30ĢØŅŅŠĶĮŖŗĻŹÕøī»ś£¬20Ģؼ׊ĶĮŖŗĻŹÕøī»śČ«²æÅÉĶłBµŲĒų£¬Ź¹øĆ¹«Ė¾50ĢØŹÕøī»śĆæĢģ»ńµĆ×ā½š×īøߣ®
±¾Ģāæ¼²éŅ»“ĪŗÆŹżµÄŠŌÖŹ£¬½āĢā¹Ų¼üŹĒĆ÷Č·ĢāŅā£¬ÕŅ³öĖłĒóĪŹĢāŠčŅŖµÄĢõ¼ž£¬ĄūÓĆŅ»“ĪŗÆŹżŗĶ²»µČŹ½µÄŠŌÖŹ½ā“š£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø±¾Š”Ģā12·Ö£©Š”Ć÷ÓŠ5ÕÅŠ“×Ų»Ķ¬Źż×ÖµÄæØʬ£¬Ēė°“ŅŖĒó³é³öæØʬ£¬Ķź³ÉĻĀĮŠø÷ĪŹĢā£ŗ
![]()
£Ø1£©“ÓÖŠČ”³ö2ÕÅæØʬ£¬Ź¹Õā2ÕÅæØʬÉĻŹż×ֵijĖ»ż×ī“ó£¬ČēŗĪ³éČ”£æ×ī“óÖµŹĒ¶ąÉŁ?
“š£ŗĪŅ³éČ”µÄ2ÕÅæØʬŹĒ ”¢ £¬³Ė»żµÄ×ī“óÖµĪŖ £®
£Ø2£©“ÓÖŠČ”³ö2ÕÅæØʬ£¬Ź¹Õā2ÕÅæØʬÉĻŹż×ÖĻą³żµÄÉĢ×īŠ”£¬ČēŗĪ³éČ”£æ×īŠ”ÖµŹĒ¶ąÉŁ?
“š£ŗĪŅ³éČ”µÄ2ÕÅæØʬŹĒ ”¢ £¬ÉĢµÄ×īŠ”ÖµĪŖ £®
£Ø3£©“ÓÖŠČ”³ö4ÕÅæØʬ£¬ÓĆѧ¹żµÄŌĖĖć·½·Ø£¬Ź¹½į¹ūĪŖ24£®ČēŗĪ³éČ”£æŠ“³öŌĖĖćŹ½×Ó£®£ØŠ“³öŅ»ÖÖ¼“æÉ£©
“š£ŗĪŅ³éČ”µÄ4ÕÅæØʬŹĒ ”¢ ”¢ ”¢ £¬
Ėć24µÄŹ½×ÓĪŖ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÖ±ĻßAB£ŗy=![]() x+
x+![]() ·Ö±š½»xÖį”¢yÖįÓŚµćB”¢AĮ½µć,C£Ø3£¬0£©£¬D”¢E·Ö±šĪŖĻ߶ĪAOŗĶĻ߶ĪACÉĻŅ»¶Æµć£¬BE½»yÖįÓŚµćH,ĒŅAD£½CE£®µ±BD£«BEµÄÖµ×īŠ”Ź±£¬ŌņHµćµÄ×ų±źĪŖ£Ø £©
·Ö±š½»xÖį”¢yÖįÓŚµćB”¢AĮ½µć,C£Ø3£¬0£©£¬D”¢E·Ö±šĪŖĻ߶ĪAOŗĶĻ߶ĪACÉĻŅ»¶Æµć£¬BE½»yÖįÓŚµćH,ĒŅAD£½CE£®µ±BD£«BEµÄÖµ×īŠ”Ź±£¬ŌņHµćµÄ×ų±źĪŖ£Ø £©

A. £Ø0£¬4£© B. £Ø0£¬5£© C. £Ø0£¬![]() £© D. £Ø0£¬
£© D. £Ø0£¬![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»ĢõÄĻ±±·½ĻņµÄ¹«Ā·ÉĻ£¬ÓŠŅ»Į¾³ö×ā³µĶ£ŌŚAµŲ£¬³Ė³µµÄµŚŅ»Ī»æĶČĖĻņÄĻ×ß3Ē§Ć×ĻĀ³µ£»øĆ³µ¼ĢŠųĻņÄĻæŖ£¬ÓÖ×ßĮĖ2Ē§Ć×ŗó£¬ÉĻĄ“µŚ¶žĪ»æĶČĖ£¬µŚ¶žĪ»æĶČĖ³Ė³µĻņ±±×ß7Ē§Ć×ĻĀ³µ£¬“ĖŹ±Ē”ŗĆÓŠµŚČżĪ»æĶČĖÉĻ³µ£¬ĻČĻņ±±×ß3Ē§Ć×£¬ÓÖµ÷Ķ·ĻņÄĻ×ߣ¬½į¹ūĻĀ³µŹ±³ö×ā³µĒ”ŗƵ½ĮĖAµŲ£®
£Ø1£©Čē¹ūŅŌAµŲĪŖŌµć£¬Ļņ±±·½ĻņĪŖÕż·½Ļņ£¬ÓĆ1øöµ„Ī»±ķŹ¾1Ē§Ć×£¬ŌŚŹżÖįÉĻ±ķŹ¾³öµŚŅ»Ī»æĶČĖŗĶµŚ¶žĪ»æĶČĖĻĀ³µµÄĪ»ÖĆ£»
£Ø2£©µŚČżĪ»æĶČĖ³Ė³µ×ßĮĖ¶ąÉŁĒ§Ć×£æ
£Ø3£©¹ę¶Ø³ö×ā³µµÄŹÕ·Ń±ź×¼ŹĒ4Ē§Ć×ÄŚø¶7ŌŖ£¬³¬¹ż4Ē§Ć׵IJæ·ÖĆæĒ§Ć×¼Óø¶1ŌŖ£Ø²»×ć1Ē§Ć×°“1Ē§Ć×Ėć£©£¬ÄĒĆ“øĆ³ö×ā³µĖ¾»śŌŚÕāČżĪ»æĶČĖÖŠ¹²ŹÕĮĖ¶ąÉŁĒ®£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖÄøö¾łÓÉŹ®ĮłøöŠ”Õż·½ŠĪ×é³ÉµÄÕż·½ŠĪĶųøńÖŠ£¬ø÷ÓŠŅ»øöČż½ĒŠĪABC£¬ÄĒĆ“ÕāĖÄøöČż½ĒŠĪÖŠ£¬²»ŹĒÖ±½ĒČż½ĒŠĪµÄŹĒ£Ø””””£©
A. 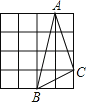 B.
B. 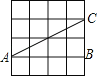 C.
C. 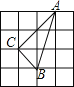 D.
D. 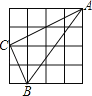
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»Į¾»õ³µ“Ó°Ł»õ“óĀ„³ö·¢øŗŌšĖĶ»õ£¬Ļņ¶«×ßĮĖ 5 Ē§Ć×µ½“ļŠ”Ć÷¼Ņ£¬¼ĢŠųĻņ¶«×ßĮĖ 1.5 Ē§Ć×µ½“ļŠ”ŗģ¼Ņ£¬Č»ŗóĻņĪ÷×ßĮĖ 9.5 Ē§Ć×µ½“ļŠ”øÕ¼Ņ£¬×īŗó·µ»Ų°Ł»õ“óĀ„£®
![]()
£Ø1£©ŅŌ°Ł»õ“óĀ„ĪŖŌµć£¬Ļņ¶«ĪŖÕż·½Ļņ£¬1 øöµ„Ī»³¤¶Č±ķŹ¾ 1 Ē§Ć×£¬ĒėÄćŌŚŹżÖįÉĻ±ź³öŠ”Ć÷”¢Š”ŗģ”¢Š”øÕ¼ŅµÄĪ»ÖĆ£®£ØŠ”Ć÷¼ŅÓƵć A ±ķŹ¾£¬Š”ŗģ¼ŅÓƵć B ±ķŹ¾£¬Š”øÕ¼ŅÓƵć C ±ķŹ¾£©
£Ø2£©Š”Ć÷¼ŅÓėŠ”øÕ¼ŅĻą¾ą¶ąŌ¶£æ
£Ø3£©Čō»õ³µĆæĒ§Ć×ŗÄÓĶ 0.6 Éż£¬ÄĒĆ“ÕāĮ¾»õ³µ“Ė“ĪĖĶ»õ¹²ŗÄÓĶ¶ąÉŁÉż£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
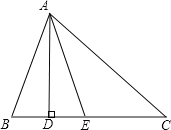
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻB£¾”ĻC£¬AD”ĶBC£¬“¹×ćĪŖD£¬AEĘ½·Ö”ĻBAC£®ŅŃÖŖ”ĻB=65”ć£¬”ĻDAE=20”ć£¬Ēó”ĻCµÄ¶ČŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬MNŹĒ°ė¾¶ĪŖ1µÄ”ŃOµÄÖ±¾¶£¬µćAŌŚ”ŃOÉĻ£¬”ĻAMN=30”ć£¬µćBĪŖĮÓ»”ANµÄÖŠµć£®PŹĒÖ±¾¶MNÉĻŅ»¶Æµć£¬ŌņPA+PBµÄ×īŠ”ÖµĪŖ£Ø £©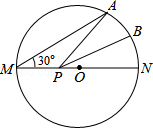
A.![]()
B.1
C.2
D.2 ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
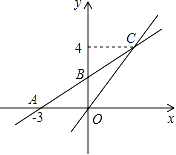
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»“ĪŗÆŹży=kx+bµÄĶ¼ĻóÓėxÖį½»µćĪŖA£Ø©3£¬0£©£¬ÓėyÖį½»µćĪŖB£¬ĒŅÓėÕż±ČĄżŗÆŹży=![]() xµÄĶ¼Ļó½»ÓŚµćC£Øm£¬4£©£®
xµÄĶ¼Ļó½»ÓŚµćC£Øm£¬4£©£®
£Ø1£©ĒómµÄÖµ¼°Ņ»“ĪŗÆŹży=kx+bµÄ±ķ“ļŹ½£»
£Ø2£©¹Ū²ģŗÆŹżĶ¼Ļó£¬Ö±½ÓŠ“³ö¹ŲÓŚxµÄ²»µČŹ½![]() x£¼kx+bµÄ½ā¼Æ£®
x£¼kx+bµÄ½ā¼Æ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com