
 如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).
如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0). 解:(1)在Rt△OAB中,
解:(1)在Rt△OAB中, ,
, cos30°=
cos30°= ,BD=
,BD= BO=
BO= ,
, ,
, );
); ,
, )、O(0,0)三点的坐标代入y=ax2+bx+c,
)、O(0,0)三点的坐标代入y=ax2+bx+c, ,
, ,
, x2+
x2+ x;
x; x2+
x2+ x)(其中0<x<
x)(其中0<x< ),使四边形ABCO面积最大,而△OAB面积为定值,
),使四边形ABCO面积最大,而△OAB面积为定值, |CF|•|OE|+
|CF|•|OE|+ |CF|•|ED|=
|CF|•|ED|= |CF|•|OD|=
|CF|•|OD|= |CF|,
|CF|, x2+
x2+ x-
x- x=-
x=- x2+
x2+ x,
x, x2+
x2+ x,
x, 时,△OBC面积最大,最大面积为
时,△OBC面积最大,最大面积为 .
. ,
, ),
), .
. ,过点B作BD垂直于x轴,垂足为D,利用已知条件可以求出OD,BD,也就求出B的坐标;
,过点B作BD垂直于x轴,垂足为D,利用已知条件可以求出OD,BD,也就求出B的坐标; x2+
x2+ x),使四边形ABCO面积最大,而△OAB面积为定值,只要△OBC面积最大,四边形ABCO面积就最大.过点C作x轴的垂线CE,垂足为E,交OB于点F,则S△OBC=S△OCF+S△BCF=
x),使四边形ABCO面积最大,而△OAB面积为定值,只要△OBC面积最大,四边形ABCO面积就最大.过点C作x轴的垂线CE,垂足为E,交OB于点F,则S△OBC=S△OCF+S△BCF= |CF|•|OE|+
|CF|•|OE|+ |CF|•|ED|=
|CF|•|ED|= |CF|•|OD|=
|CF|•|OD|= |CF|,而|CF|=yC-yF=-
|CF|,而|CF|=yC-yF=- x2+
x2+ x-
x- x=-
x=- x2+
x2+ x,这样可以得到S△OBC=-
x,这样可以得到S△OBC=- x2+
x2+ x,利用二次函数就可以求出△OBC面积最大值,也可以求出C的坐标.
x,利用二次函数就可以求出△OBC面积最大值,也可以求出C的坐标.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
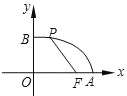 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-| 3 |
| 5 |
| A、OB=3 | B、OA=5 |
| C、AF=2 | D、BF=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•黄冈模拟)如图,已知点F的坐标为(3,0),点A,B分别是以y轴为对称轴的某二次函数部分图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
(2012•黄冈模拟)如图,已知点F的坐标为(3,0),点A,B分别是以y轴为对称轴的某二次函数部分图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-| 3 |
| 5 |
| 16 |
| 25 |
| 16 |
| 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).
如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).查看答案和解析>>
科目:初中数学 来源:2007年广东省汕尾市陆丰市玉燕中学中考数学模拟试卷(2月份)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com