解:(1)存在这样的抛物线F,使得|OA|
2=|OB|•|OC|.
理由是:∵平移y=-tx
2的图象得到的抛物线F的顶点为Q,
∴抛物线F对应的解析式为:y=-t(x-t)
2+b,即y=-tx
2+2t
2x-t
3+b,
令y=0,得OB=t-
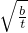
,OC=t+
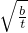
,
∴|OB|•|OC|=|(t-
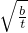
)(t+
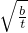
)|=|t
2-
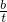
|=t
2=OA
2,
即
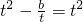
,
所以当b=2t
3时,存在抛物线F使得|OA|
2=|OB|•|OC|,
即:存在这样的抛物线F,使得|OA|
2=|OB|•|OC|.
(2)∵AQ∥BC,
∴t=b,得:y=-t(x-t)
2+t,
解得x
1=t-1,x
2=t+1.
在Rt△AOB中,
①当t>0时,由|OB|<|OC|,得B(t-1,0),
当t-1>0时,由tan∠ABO=

=
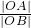
=
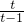
,解得t=3,
此时,二次函数解析式为y=-3x
2+18x-24;
当t-1<0时,由tan∠ABO=

=
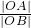
=
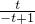
,解得t=

,
此时,二次函数解析式为y=-

x
2+
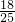
x+
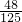
;
②当t<0时,由|OB|<|OC|,将-t代替t,解得:t=-

,t=-3,
同法求出y=-

x
2+
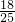
x-
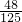
或y=-3x
2+18x+24;
故二次函数解析式为y=-

x
2+
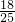
x-
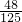
或y=-3x
2+18x+24,
答:抛物线F对应的二次函数的解析式是y=-

x
2+
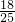
x±
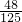
或y=-3x
2+18x±24.
分析:(1)平移二次函数y=-tx
2的图象,得到的抛物线F,则抛物线的二次项系数不变,顶点为Q,则函数的解析式就可以直接写出.是y=-t(x-t)
2+b.|OB|•|OC|就是一元二次方程-t(x-t)
2+b=0的两根的积得绝对值,因而可以用根据韦达定理,利用t表示出来.而OA=t,根据|OA|
2=|OB|•|OC|就可以得到一个关于t的方程.从而把问题转化为判断方程的解得问题.
(2)AQ∥BC即Q得纵坐标是b=t,得到抛物线F是:y=-t(x-t)
2+t.就可以求出B,C的坐标.已知tan∠ABO=

,就是已知OA与OB得比值,即t的关系.就可以转化为方程问题解决.
点评:我们可以先假设存在这样的抛物线,如果能够求出对应的值,则存在,如果求不出,则不存在.

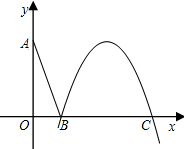 函数y=-tx2的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(|OB|<|OC|).连接AB.
函数y=-tx2的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(|OB|<|OC|).连接AB. ,求抛物线F对应的二次函数的解析式.
,求抛物线F对应的二次函数的解析式.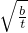 ,OC=t+
,OC=t+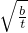 ,
,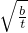 )(t+
)(t+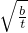 )|=|t2-
)|=|t2-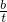 |=t2=OA2,
|=t2=OA2,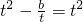 ,
, =
=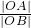 =
=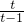 ,解得t=3,
,解得t=3, =
=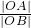 =
=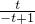 ,解得t=
,解得t= ,
, x2+
x2+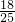 x+
x+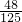 ;
; ,t=-3,
,t=-3, x2+
x2+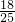 x-
x-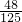 或y=-3x2+18x+24;
或y=-3x2+18x+24; x2+
x2+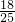 x-
x-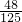 或y=-3x2+18x+24,
或y=-3x2+18x+24, x2+
x2+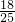 x±
x±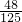 或y=-3x2+18x±24.
或y=-3x2+18x±24. ,就是已知OA与OB得比值,即t的关系.就可以转化为方程问题解决.
,就是已知OA与OB得比值,即t的关系.就可以转化为方程问题解决.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
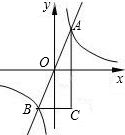 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y= (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.