
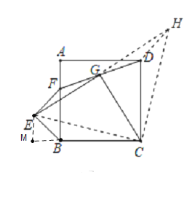
【题目】如图,已知正方形ABCD中,以BF为底向正方形外侧作等腰直角三角形BEF,连接DF,取DF的中点G,连接EG,CG.

(1)如图1,当点A与点F重合时,猜想EG与CG的数量关系为 ,EG与CG的位置关系为 ,请证明你的结论.
(2)如图2,当点F在AB上(不与点A重合)时,(1)中结论是否仍然成立?请说明理由;如图3,点F在AB的左侧时,(1)中的结论是否仍然成立?直接做出判断,不必说明理由.
(3)在图2中,若BC=4,BF=3,连接EC,求![]() 的面积.
的面积.
【答案】(1)EG=CG,EG⊥CG;(2)当点F在AB上(不与点A重合)时,(1)中结论仍然成立,理由见解析,点F在AB的左侧时,(1)中的结论仍然成立;(3)S△CEG=![]() .
.
【解析】
(1)过E作EM⊥AD交AD的延长线于M,证明△AME是等腰直角三角形,得出AM=EM=![]() AE=
AE=![]() AB,证出DG=AG=
AB,证出DG=AG=![]() AD=AM=EM,得出GM=CD,证明△GEM≌△CGD(SAS),得出EG=CG,∠EGM=∠GCD,证出∠CGE=180°-90°=90°,即可得出EG⊥CG;
AD=AM=EM,得出GM=CD,证明△GEM≌△CGD(SAS),得出EG=CG,∠EGM=∠GCD,证出∠CGE=180°-90°=90°,即可得出EG⊥CG;
(2)延长EG至H,使HG=EG,连接DH、CH、CE,证明△EFG≌△HDG(SAS),得出EF=HD,∠EFG=∠HDG,证明△CBE≌△CDH(SAS),得出CE=CH,∠BCE=∠DCH,得出∠ECH=∠BCD=90°,证明△ECH是等腰直角三角形,得出CG=![]() EH=EG,EG⊥CG;延长EG至H,使HG=EG,连接DH、CH、CE,同理可证CG=
EH=EG,EG⊥CG;延长EG至H,使HG=EG,连接DH、CH、CE,同理可证CG=![]() EH=EG,EG⊥CG;
EH=EG,EG⊥CG;
(3)作EM垂直于CB的延长线与M,先求出BM,EM的值,即可根据勾股定理求出CE的长度,从而求出CG的长,即可求出面积.
解:(1)EG=CG,EG⊥CG;理由如下:
过E作EM⊥AD交AD的延长线于M,如图1所示:
则∠M=90°,
∵四边形ABCD是正方形,
∴AB=AD=CD,∠BAD=∠D=90°,
∴∠BAM=90°,
∵△BEF是等腰直角三角形,
∴∠BAE=45°,AE=![]() AB,
AB,
∴∠MAE=45°,
∴△AME是等腰直角三角形,
∴AM=EM=![]() AE=
AE=![]() AB,
AB,
∵G是DF的中点,
∴DG=AG=![]() AD=AM=EM,
AD=AM=EM,
∴GM=CD,
在△GEM和△CGD中,
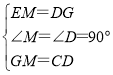 ,
,
∴△GEM≌△CGD(SAS),
∴EG=CG,∠EGM=∠GCD,
∵∠GCD+∠DGC=90°,
∴∠EGM+∠DGC=90°,
∴∠CGE=180°-90°=90°,
∴EG⊥CG;
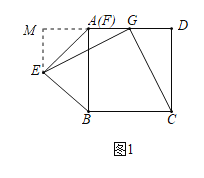
(2)当点F在AB上(不与点A重合)时,(1)中的结论仍然成立,理由如下:
延长EG至H,使HG=EG,连接DH、CH、CE,如图2所示:
∵G是DF的中点,
∴FG=DG,
在△EFG和△HDG中, ,
,
∴△EFG≌△HDG(SAS),
∴EF=HD,∠EFG=∠HDG,
∵△BEF是等腰直角三角形,
∴EF=BE,∠BFE=∠FBE=45°,
∴BE=DH,
∵四边形ABCD是正方形,
∴AB∥CD,∠ABC=∠BCD=90°,BC=CD,
∴∠AFD=∠CDG,
∴∠AFE=∠CDH=135°,
∵∠CBE=90°+45°=135°,
∴∠CBE=∠CDH,
在△CBE和△CDH中,
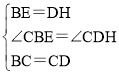 ,
,
∴△CBE≌△CDH(SAS),
∴CE=CH,∠BCE=∠DCH,
∴∠ECH=∠BCD=90°,
∴△ECH是等腰直角三角形,
∵EG=HG,
∴CG=![]() EH=EG,EG⊥CG;
EH=EG,EG⊥CG;

点F在AB的左侧时,(1)中的结论仍然成立,理由如下:
延长EG至H,使HG=EG,连接DH、CH、CE,如图3所示:
∵G是DF的中点,
∴FG=DG,
在△EFG和△HDG中,
 ,
,
∴△EFG≌△HDG(SAS),
∴EF=HD,∠EFG=∠HDG,
∵△BEF是等腰直角三角形,
∴EF=BE,∠BEF=90°,
∴BE=DH,
∵四边形ABCD是正方形,
∴AB∥CD,∠ABC=∠BCD=90°,BC=CD,
∴∠BNF=∠CDG,
∵∠EFG+∠BNF+∠BEF+∠ABE=∠HDG+∠CDG+∠CDH=360°,
∴∠BEF+∠ABE=∠CDH,
∴∠ABC+∠ABE=∠CDH,即∠CBE=∠CDH,
在△CBE和△CDH中,
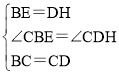 ,
,
∴△CBE≌△CDH(SAS),
∴CE=CH,∠BCE=∠DCH,
∴∠ECH=∠BCD=90°,
∴△ECH是等腰直角三角形,
∵EG=HG,
∴CG=![]() EH=EG,EG⊥CG;
EH=EG,EG⊥CG;

(3)如下图所示:作EM垂直于CB的延长线与M,
∵△BEF为等腰直角三角形,BF=3,
∴BE=![]() ,∠ABE=45°,
,∠ABE=45°,
∵EM⊥BM,AB⊥CM,
∴∠EBM=45°,
∴△EMB为等腰直角三角形,
∴EM=BM=![]() ,
,
∵BC=4,
∴CM=![]() ,
,
∴CE=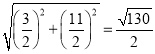 ,
,
由(2)知,△GEC为等腰直角三角形,
∴CG=EG=![]() ,
,
∴S△CEG=![]() .
.


科目:初中数学 来源: 题型:
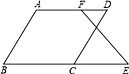
【题目】完成下面推理过程:
如图,已知∠B+∠BCD=180°,∠B=∠D.求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°,
∴AB∥ ( )
∴∠B=∠DCE( )
又∵∠B=∠D,
∴∠DCE=∠D( )
∴ ∥ ( )
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(
两点(![]() 左
左![]() 右),与
右),与![]() 轴交于
轴交于![]() 点
点![]() .
.
(![]() )求
)求![]() 的值.
的值.
(![]() )若
)若![]() 为二次函数
为二次函数![]() 图象的顶点,求证:
图象的顶点,求证: ![]() .
.
(![]() )若
)若![]() 为二次函数
为二次函数![]() 图象上一点,且
图象上一点,且![]() ,求
,求![]() 点的坐标.
点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P是三角形ABC内一点,射线PD∥AC,射线PE∥AB.
(1)当点D,E分别在AB,BC上时,
①补全图1;
②猜想∠DPE与∠A的数量关系,并证明;
(2)当点D,E都在线段BC上时,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四名同学进行一次乒乓球单打比赛,要从中选两位同学打第一场比赛.
(1)请用树状图或列表法求恰好选中甲、乙两位同学的概率;
(2)请利用若干个除颜色外其余都相同的乒乓球,设计一个摸球的实验(至少摸两次),
并根据该实验写出一个发生概率与(1)所求概率相同的事件.
查看答案和解析>>
科目:初中数学 来源: 题型:
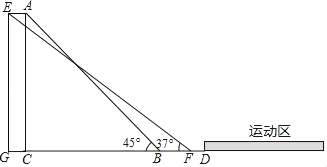
【题目】某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 其中所有正确结论的序号是( )
其中所有正确结论的序号是( )
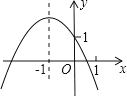
A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎解方程![]() 时出现了错误,其解答过程如下:
时出现了错误,其解答过程如下:
解:方程两边都乘以![]() ,得
,得![]() ,(第1步)
,(第1步)
移项,合并同类项,得![]() ,(第2步)
,(第2步)
经检验,![]() 是原方程的解.(第3步)
是原方程的解.(第3步)
(1)小马虎解答过程是从第______步开始出错的,出错的原因是___________;
(2)请写出此题正确的解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com