【答案】
分析:(1)求∠OAB的度数,我们可根据A、B的坐标来求,根据tan∠OAB=B的纵坐标的绝对值:A、B横坐标的差的绝对值,可得出∠OAB的度数.得出的∠BAO是60°后,以及折叠得到的AT=A′T,那么三角形A′AT是等边三角形,且三边长均为10-t.求面积就要有底边和高,我们可以AA′为底边,那么PT就是高,AA′=10-t,那么关键是PT的值,已知了∠BAT的度数,我们可以用AT的长以及∠BAT的正弦函数表示出PT的长,由此可根据三角形的面积公式得出关于S,t的函数关系式.此时AT即AA′的最大值为AB的长,也就是4,因此AT的取值范围是0<AT≤4,那么t的取值范围就是6≤t<10;
(2)当重叠部分是四边形时,那么此时A′应该在AB的延长线上,那么此时AA′的最小值应该是AB的长即4,最大的值应该是当P与B重合时AA′的值即8,由于三角形ATA′是个等边三角形,那么AT的取值范围就是4<AT<8,那么t的取值就应是2<t<6;
(3)可分成三种情况进行讨论:
①当A′在AB上时,即当6≤t<10时,可根据(1)的函数来求出此时S的最大值;
②当A′在AB延长线上但P在AB上时,即当2≤t<6时,此时重合部分的面积=三角形AA′T的面积-上面的小三角形的面积,根据AT和AB的长,我们可得出A′B的长,然后按(1)的方法即可得出上面的小三角形的面积,也就可以求出重合部分的面积;
③当A′在AB延长线上且P也在AB延长线上时,即当0<t≤2时,重合部分的面积就是三角形EFT的面积(其中E是TA′与CB的交点,F是TA与CB的交点)那么关键是求出BF,BE的值,知道了AT的长,也就知道了AP,A′P的长,根据AB=4我们不难得出BP的长,有了BP的长就可以求出A′B,BE的长,在直角三角形BPE中,可根据∠PBF的度数,和BP的长,来表示出BF的长,这样我们就能表示出EF的长了,又知道EF边上的高是OC的长,因此可根据三角形的面积来求出S的值.
然后综合三种情况判断出是否有S的最大值.
解答:解:(1)∵A,B两点的坐标分别是A(10,0)和B(8,2

),
∴tan∠OAB=
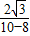
=
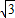
,
∴∠OAB=60°,

当点A′在线段AB上时,
∵∠OAB=60°,TA=TA′,
∴△A′TA是等边三角形,且TP⊥AA′,
∴TP=(10-t)sin60°=
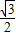
(10-t),A′P=AP=

AT=

(10-t),
∴S=S
△ATP=

A′P•TP=
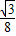
(10-t)
2,
当A´与B重合时,AT=AB=
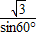
=4,
所以此时6≤t<10;
(2)当点A′在线段AB的延长线上,且点P在线段AB(不与B重合)上时,
纸片重叠部分的图形是四边形(如图①,其中E是TA′与CB的交点),
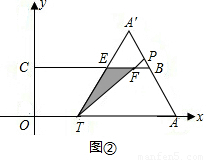
假设点P与B重合时,AT=2AB=8,点T的坐标是(2,0),由(1)中求得当A´与B重合时,T的坐标是(6,0),
则当纸片重叠部分的图形是四边形时,2<t<6;
(3)S存在最大值.
①当6≤t<10时,S=
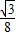
(10-t)
2,
在对称轴t=10的左边,S的值随着t的增大而减小,
∴当t=6时,S的值最大是2
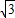
;
②当2≤t<6时,由图①,重叠部分的面积S=S
△A′TP-(S
△A′EB-S
△PFB),
∵△A′EB的高是A′B•sin60°,
∴S=
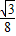
(10-t)
2-

(10-t-4)
2×
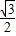
+

(
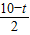
-4)
2×
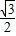
=
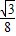
(-

t
2+2t+30)=-
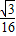
(t-2)
2+4

,
当t=2时,S的值最大是4
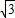
;
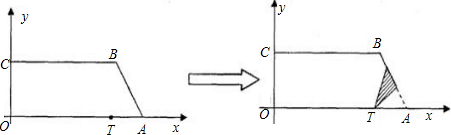
③当0<t≤2,即当点A′和点P都在线段AB的延长线上是(如图②,其中E是TA´与CB的交点,F是TP与CB的交点),
∵∠EFT=∠FTP=∠ETF,四边形ETAB是等腰梯形,
∴EF=ET=AB=4,
∴S=

EF•OC=

×4×2
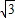
=4
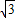
.
综上所述,S的最大值是4
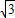
,此时t的值是t=2.
点评:这是试卷的压轴题,考查知识点较多,是代数与几何结合的综合题,其中有分类思想的渗透.
主要问题是在解题中计算三角形面积时没有除以2,或分类情况不全面,或对于取值范围的处理不到位.特别是认为只存在一个t的值使得面积最大,导致失分较多.更多是缺乏对复杂问题的分析能力,导致不会做.

 ),C(0,2
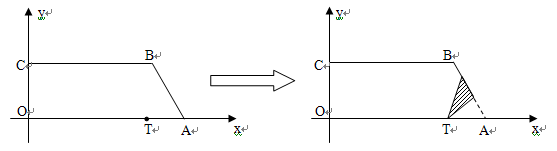
),C(0,2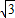 ),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S.
),点T在线段OA上(不与线段端点重合),将纸片折叠,使点A落在射线AB上(记为点A′),折痕经过点T,折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S.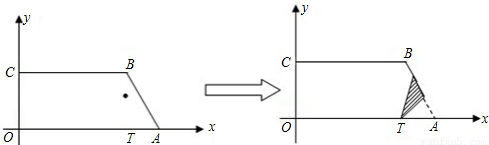
 ),
),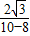 =
=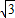 ,
,
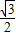 (10-t),A′P=AP=
(10-t),A′P=AP= AT=
AT= (10-t),
(10-t), A′P•TP=
A′P•TP=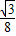 (10-t)2,
(10-t)2,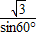 =4,
=4,
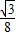 (10-t)2,
(10-t)2,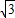 ;
;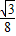 (10-t)2-
(10-t)2- (10-t-4)2×
(10-t-4)2×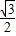 +
+ (
(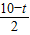 -4)2×
-4)2×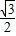 =
=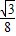 (-
(- t2+2t+30)=-
t2+2t+30)=-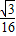 (t-2)2+4
(t-2)2+4 ,
,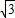 ;
; EF•OC=
EF•OC= ×4×2
×4×2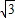 =4
=4 .
. ,此时t的值是t=2.
,此时t的值是t=2.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案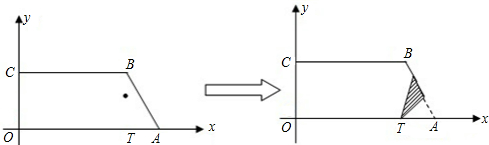

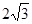 ),C(0,
),C(0,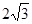 ),点T在线段OA上(不与线段端点重合),将纸片沿过T点的直线折叠,使点A落在射线AB上(记为点A′),折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;
),点T在线段OA上(不与线段端点重合),将纸片沿过T点的直线折叠,使点A落在射线AB上(记为点A′),折痕TP与射线AB交于点P,设点T的横坐标为t,折叠后纸片重叠部分(图中的阴影部分)的面积为S;