
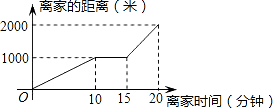
 某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离S(米)与离家时间t(分)之间的函数关系.下列说法中正确的个数是( )
某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.图中描述了他上学的途中离家距离S(米)与离家时间t(分)之间的函数关系.下列说法中正确的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
科目:初中数学 来源: 题型:选择题
 如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )
如图,周长为34cm的长方形ABCD被分成7个形状大小完全相同的小长方形,则长方形ABCD的面积为( )| A. | 49cm2 | B. | 74cm2 | C. | 68cm2 | D. | 70cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=2x上有一点A,点A的横坐标为2,直线y=kx+b经过点A与x轴正半轴交于点B.△AOB的面积为10,点P是线段OA上一动点,过点P作PH∥x轴交线段AB于H,点P的纵坐标为m.
如图,在平面直角坐标系中,直线y=2x上有一点A,点A的横坐标为2,直线y=kx+b经过点A与x轴正半轴交于点B.△AOB的面积为10,点P是线段OA上一动点,过点P作PH∥x轴交线段AB于H,点P的纵坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时).
最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD=( )| A. | 22.5° | B. | 30° | C. | 36° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com