
 DB.
DB.

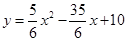 ;(2)∠ECB的大小不变.90°;(3)证明见解析;(4)∠APC>45°.
;(2)∠ECB的大小不变.90°;(3)证明见解析;(4)∠APC>45°.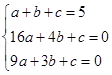 ,解得:
,解得: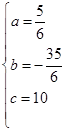 ;
;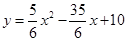 ;
; DB,
DB, BD,连接CF、BF.
BD,连接CF、BF.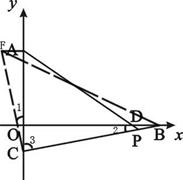


科目:初中数学 来源:不详 题型:解答题
 )秒.
)秒.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
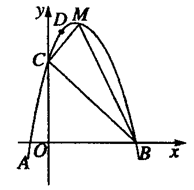
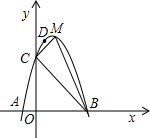
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
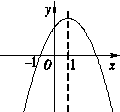
A. |
B.当 时,y随x的增大而增大 时,y随x的增大而增大 |
C. |
D. 是一元二次方程 是一元二次方程 的一个根 的一个根 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
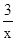 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )| A.0<x0<1 |
| B.1<x0<2 |
| C.2<x0<3 |
| D.﹣1<x0<0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com