
【题目】有一边是另一边的![]() 倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的夹角叫做智慧角.
倍的三角形叫做智慧三角形,这两边中较长边称为智慧边,这两边的夹角叫做智慧角.
(1)已知![]() 为智慧三角形,且
为智慧三角形,且![]() 的一边长为,则该智慧三角形的面积为_________;
的一边长为,则该智慧三角形的面积为_________;
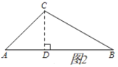
(2)如图①,在![]() 中,
中,![]() ,
,![]() ,求证:
,求证:![]() 是智慧三角形;
是智慧三角形;
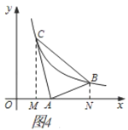
(3)如图②,![]() 是智慧三角形,
是智慧三角形,![]() 为智慧边,
为智慧边,![]() 为智慧角,
为智慧角,![]() ,点
,点![]() 在函数
在函数![]() (
(![]() )的图象上,点
)的图象上,点![]() 在点
在点![]() 的上方,且点
的上方,且点![]() 的纵坐标为
的纵坐标为![]() ,当
,当![]() 是直角三角形时,求
是直角三角形时,求![]() 的值.
的值.

【答案】(1)![]() ,
,![]() ,1,
,1,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 或
或![]()
【解析】
(1)由于不确定![]() 是哪条边的边长,故需分3种情况讨论,每种情况中,不确定长
是哪条边的边长,故需分3种情况讨论,每种情况中,不确定长![]() 的边是否为智慧边,故又需要分类讨论;
的边是否为智慧边,故又需要分类讨论;
(2)过C作AB边的垂线CD,构造两个有特殊角的直角三角形,即能用CD把各边关系表示出来,易得BC是AC的![]() 倍,即可得证;
倍,即可得证;
(3)由题意可知![]() ,因此当△ABC为直角三角形时,AB不可能为斜边,即只分
,因此当△ABC为直角三角形时,AB不可能为斜边,即只分![]() 或
或![]() ,两种情况讨论,做辅助线构造三垂直模型,证得相似或全等三角形,再利用对应边的关系把B、C的坐标表示出来,再代入
,两种情况讨论,做辅助线构造三垂直模型,证得相似或全等三角形,再利用对应边的关系把B、C的坐标表示出来,再代入![]() 计算.
计算.
解:(1)如图2,设![]()
①若![]()
1)![]()
![]()
2)![]() ,则
,则![]()
![]()
②若![]()
1)![]() ,即
,即![]()
![]()
2)![]() ,则
,则![]()
![]()
③若![]() ,则
,则![]()
![]()
故答案为:![]() ,
,![]() ,1,
,1,![]()
(2)如图2,过点![]() 作
作![]() 于点
于点![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() 是智慧三角形.
是智慧三角形.
(3)由题意可知![]() 或
或![]() .
.
①当![]() 时,如图3,
时,如图3,
过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵点![]() 在函数
在函数![]() 的图象上,
的图象上,
∴![]() .
.
解得:![]() ,
,![]() (舍去).
(舍去).
∴![]() .
.
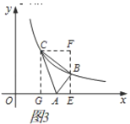
②当![]() 时,如图4,过点
时,如图4,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
则![]() .
.
∴![]() .
.
∴![]() .
.
由(1)知![]() .
.
∴![]() 是等腰直角三角形.
是等腰直角三角形.
∴![]() .由①知
.由①知![]() .
.
∴![]() .
.
∴![]() .
.
设![]() ,则
,则![]() .
.
∴![]() ,
,![]() .
.
∵点![]() 在函数
在函数![]() (
(![]() )的图象上,
)的图象上,
![]() .
.
解得:![]() .
.
∴![]() .
.
综上所述,![]() 或
或![]() .
.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,小明想测量斜坡![]() 旁一棵垂直于地面
旁一棵垂直于地面![]() 的树
的树![]() 的高度,他们先在点
的高度,他们先在点![]() 处测得树顶
处测得树顶![]() 的仰角为
的仰角为![]() ,然后在坡顶
,然后在坡顶![]() 测得树顶
测得树顶![]() 的仰角为
的仰角为![]() ,已知斜坡
,已知斜坡![]() 的长度为
的长度为![]() ,斜坡顶点
,斜坡顶点![]() 到地面的垂直高度
到地面的垂直高度![]() ,则树
,则树![]() 的高度是( )
的高度是( )![]()
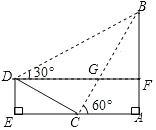
A. 20![]() B. 30
B. 30![]() C. 30D. 40
C. 30D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
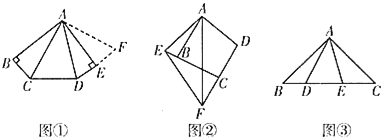
【题目】(1)操作发现
如图①,在五边形![]() 中,
中,![]() ,
,![]() ,试猜想
,试猜想![]() 之间的数量关系,小明经过仔细思考,得到如下解题思路:将
之间的数量关系,小明经过仔细思考,得到如下解题思路:将![]() 绕点
绕点![]() 逆时针旋转90°至
逆时针旋转90°至![]() ,由
,由![]() ,得
,得![]() ,即点
,即点![]() 三点共线,易证
三点共线,易证![]() ,故
,故![]() 之间的数量关系是________;
之间的数量关系是________;
(2)类比探究
如图②,在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 分别在边
分别在边![]() 的延长线上,
的延长线上,![]() ,连接
,连接![]() ,试猜想
,试猜想![]() 之间的数量关系,并给出证明;
之间的数量关系,并给出证明;
(3)拓展延伸
如图③,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 均在边
均在边![]() 上,且
上,且![]() ,若
,若![]() ,则
,则![]() 的长为________.
的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() ,
,![]() 轴,
轴,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第四象限.点
在第四象限.点![]() 是
是![]() 边上的一个动点.
边上的一个动点.
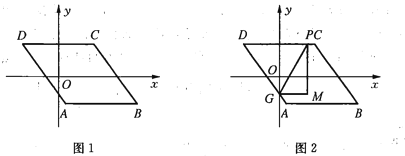
(1)若点![]() 在边
在边![]() 上,
上,![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若点![]() 在边
在边![]() 或
或![]() 上,点
上,点![]() 关于一条坐标轴对称的点
关于一条坐标轴对称的点![]() 落在直线
落在直线![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)若点![]() 在边
在边![]() 、
、![]() 或
或![]() 上,点
上,点![]() 是
是![]() 与
与![]() 轴的交点,如图2,过点
轴的交点,如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,它们相交于点
,它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标(直接写出答案).
的坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为6元/![]() .在乙批发店,一次购买数量不超过
.在乙批发店,一次购买数量不超过![]() 时,价格为7元/
时,价格为7元/![]() ;一次购买数量超过
;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格仍为7元/
的价格仍为7元/![]() ,超过
,超过![]() 部分的价格为5元/
部分的价格为5元/![]() .设小王在同一个批发店一次购买苹果的数量为
.设小王在同一个批发店一次购买苹果的数量为![]() .
.
(Ⅰ)根据题意填空:
①若一次购买数量为![]() 时,在甲批发店的花费为________元,在乙批发店的花费为________元;
时,在甲批发店的花费为________元,在乙批发店的花费为________元;
②若一次购买数量为![]() 时,在甲批发店的花费为________元,在乙批发店的花费为________元;
时,在甲批发店的花费为________元,在乙批发店的花费为________元;
(Ⅱ)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空:
①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为_________![]() ;
;
②若小王在同一个批发店一次购买苹果的数量为![]() ,则他在甲、乙两个批发店中的________批发店购买花费少;
,则他在甲、乙两个批发店中的________批发店购买花费少;
③若小王在同一个批发店一次购买苹果花费了260元,则他在甲、乙两个批发店中的_________批发店购买数量多.
查看答案和解析>>
科目:初中数学 来源: 题型:
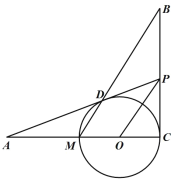
【题目】如图,已知BCAC,圆心O在AC上,点M与点C分别是AC与⊙O的交点,点D是MB与⊙O的交点,点P是AD延长线与BC的交点,且ADAOAMAP,连接OP.
(1)证明:MD//OP;
(2)求证:PD是⊙O的切线;
(3)若AD24,AMMC,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1 ,用篱笆靠墙围成矩形花圃ABCD ,墙可利用的最大长度为15m,一面利用旧墙 ,其余三面用篱笆围,篱笆总长为24m,设平行于墙的BC边长为x m
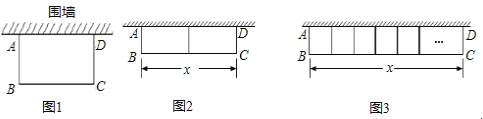
(1)若围成的花圃面积为40m2时,求BC的长
(2)如图2,若计划在花圃中间用一道篱笆隔成两个小矩形,且围成的花圃面积为50m2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由.
(3)如图3,若计划在花圃中间用n道篱笆隔成小矩形,且当这些小矩形为正方形时,请列出x、n满足的关系式
查看答案和解析>>
科目:初中数学 来源: 题型:
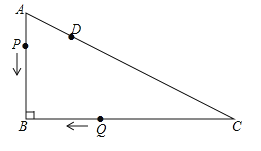
【题目】如图,Rt△ABC中,∠B=90°,AB=3cm,BC=4cm.点D在AC上,AD=1cm,点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了2cm,并沿B→C→A的路径匀速运动;点Q保持速度不变,并继续沿原路径匀速运动,两点在D点处再次相遇后停止运动,设点P原来的速度为xcm/s.
(1)点Q的速度为 cm/s(用含x的代数式表示).
(2)求点P原来的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com