
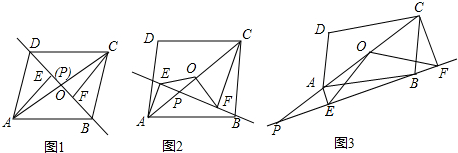
分析 (1)由△AOE≌△COF即可得出结论.
(2)图2中的结论为:CF=OE+AE,延长EO交CF于点G,只要证明△EOA≌△GOC,△OFG是等边三角形,即可解决问题.
图3中的结论为:CF=OE-AE,延长EO交FC的延长线于点G,证明方法类似.
解答 解:(1)∵AE⊥PB,CF⊥BP,
∴∠AEO=∠CFO=90°,
在△AEO和△CFO中,
$\left\{\begin{array}{l}{∠AEO=∠CFO}\\{∠AOE=∠COF}\\{AO=OC}\end{array}\right.$,
∴△AOE≌△COF,
∴OE=OF.
(2)图2中的结论为:CF=OE+AE.
图3中的结论为:CF=OE-AE.
选图2中的结论证明如下:
延长EO交CF于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠EAO=∠GCO,
在△EOA和△GOC中,
$\left\{\begin{array}{l}{∠EAO=∠GCO}\\{AO=OC}\\{∠AOE=∠COG}\end{array}\right.$,
∴△EOA≌△GOC,
∴EO=GO,AE=CG,
在Rt△EFG中,∵EO=OG,
∴OE=OF=GO,
∵∠OFE=30°,
∴∠OFG=90°-30°=60°,
∴△OFG是等边三角形,
∴OF=GF,
∵OE=OF,
∴OE=FG,
∵CF=FG+CG,
∴CF=OE+AE.
选图3的结论证明如下:
延长EO交FC的延长线于点G,
∵AE⊥BP,CF⊥BP,
∴AE∥CF,
∴∠AEO=∠G,
在△AOE和△COG中,
$\left\{\begin{array}{l}{∠AEO=∠G}\\{∠AOE=∠GOC}\\{AO=OC}\end{array}\right.$,
∴△AOE≌△COG,
∴OE=OG,AE=CG,
在Rt△EFG中,∵OE=OG,
∴OE=OF=OG,
∵∠OFE=30°,
∴∠OFG=90°-30°=60°,
∴△OFG是等边三角形,
∴OF=FG,
∵OE=OF,
∴OE=FG,
∵CF=FG-CG,
∴CF=OE-AE.
点评 本题考查四边形综合题、全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
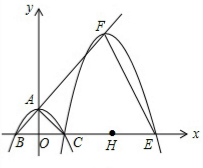 如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.
如图,抛物线y=ax2+c(a≠0)与y轴交于点A,与x轴交于点B,C两点(点C在x轴正半轴上),△ABC为等腰直角三角形,且面积为4.现将抛物线沿BA方向平移,平移后的抛物线经过点C时,与x轴的另一交点为E,其顶点为F,对称轴与x轴的交点为H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
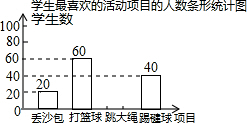 我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:
我市某中学决定在学生中开展丢沙包、打篮球、跳大绳和踢毽球四种项目的活动,为了解学生对四种项目的喜欢情况,随机调查了该校m名学生最喜欢的一种项目(每名学生必选且只能选择四种活动项目的一种),并将调查结果绘制成如下的不完整的统计图表:| 项目 | 学生数(名) | 百分比 |
| 丢沙包 | 20 | 10% |
| 打篮球 | 60 | p% |
| 跳大绳 | n | 40% |
| 踢毽球 | 40 | 20% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{a}$+$\sqrt{b}$=$\sqrt{ab}$ | B. | (-a2)2=-a4 | C. | (a-2)2=a2-4 | D. | $\sqrt{a}$÷$\sqrt{b}$=$\sqrt{\frac{a}{b}}$(a≥0,b>0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com