
分析 先去掉小括号,再去掉中括号,最后进行分解因式后并约分即可.
解答 解:ab[$\frac{b}{{a}^{2}+2ab+{b}^{2}}×(1+\frac{b}{a})-\frac{a}{ab+{b}^{2}}$],
=ab[$\frac{b}{(a+b)^{2}}$×$\frac{a+b}{a}$-$\frac{a}{b(a+b)}$],
=ab[$\frac{b}{a(a+b)}$-$\frac{a}{b(a+b)}$],
=$\frac{{b}^{2}}{a+b}$-$\frac{{a}^{2}}{a+b}$,
=$\frac{{b}^{2}-{a}^{2}}{a+b}$,
=$\frac{(b-a)(b+a)}{a+b}$,
=b-a;
故答案为:b-a.
点评 本题考查了分式的混合运算,解答本题的关键在于熟练掌握分式混合运算的运算法则,分解因式是基础.


科目:初中数学 来源: 题型:填空题
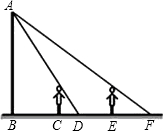 如图,李明晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知李明的身高是1.5米,则BC=3米.
如图,李明晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知李明的身高是1.5米,则BC=3米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k≥-1 | B. | k>-1 | C. | k$≥-\frac{1}{2}$ | D. | k$>-\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
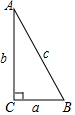 在Rt△ABC中,∠C=90°.
在Rt△ABC中,∠C=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
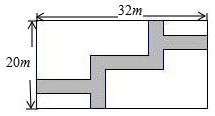 如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )
如图,在宽度为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪,要使草坪的面积为540m2,求道路的宽.如果设小路宽为xm,根据题意,所列方程正确的是( )| A. | (20+x)(32-x)=540 | B. | (20-x)(32-x)=100 | C. | (20-x)(32-x)=540 | D. | (20+x)(32-x)=540 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{90}{x+2}$=$\frac{60}{x-2}$ | B. | $\frac{90}{x-2}$=$\frac{60}{x+2}$ | C. | $\frac{90}{x}$+2=$\frac{60}{x}$ | D. | $\frac{60}{x}$+2=$\frac{90}{x}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com