

分析 (1)根据三角形的面积公式求出B、C两点坐标,代入抛物线解析式解方程组即可解决问题.
(2)设直线PB解析式为y=kx+b,把P(t,-$\frac{1}{2}$t2+2),B(2,0)代入,解方程组即可.
(3)如图2中,作P关于y轴的对称点P′,连接CP′,PP′,QP′,PP′交y轴于F,PQ与OF交于点E,作P′Q′⊥CQ于Q′.只要证明∠OBD=45°,求出直线PB的解析式,解方程组即可解决问题.
解答 解:(1)如图1中,设OB=OC=OA=m,
∵$\frac{1}{2}$•2m•m=4,
∴m=2,
∴点B坐标(2,0),C(0,2),代入抛物线解析式得到$\left\{\begin{array}{l}{4a+c=0}\\{c=2}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{c=2}\end{array}\right.$.
(2)如图1中,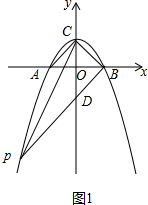
设直线PB解析式为y=kx+b,把P(t,-$\frac{1}{2}$t2+2),B(2,0)代入得$\left\{\begin{array}{l}{2k+b=0}\\{tk+b=-\frac{1}{2}{t}^{2}+2}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-\frac{t+2}{2}}\\{b=t+2}\end{array}\right.$,
∴直线PB的解析式为y=-$\frac{t+2}{2}$x+t+2,
∴点D的坐标为t+2,
∴d=-t.(t<-2).
(3)如图2中,作P关于y轴的对称点P′,连接CP′,PP′,QP′,PP′交y轴于F,PQ与OF交于点E,作P′Q′⊥CQ于Q′.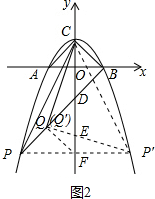
根据对称性可知:∠PCD=∠P′CD,PC=CP′,
∵PC=$\sqrt{2}$CQ,2∠PCD-∠PCQ=45°,
∴∠P′CQ=45°,CP′=$\sqrt{2}$CQ′,
∴Q与Q′重合,
∴△CQP′是等腰直角三角形,
∴∠CQE=∠EFP′=90°,∵∠CEQ=∠FEP′,
∴∠DCQ=∠FP′Q,
∵CD=PF=FP′(由2可知),
∴△CDQ≌△P′FQ,
∴DQ=QF,∠CQD=∠P′QF,
∴∠DQF=∠CQP′=90°,
∴△DQF是等腰直角三角形,
∴∠QDF=∠ODB=∠OBD=45°,
∴直线BD的解析式为y=x-2,
由$\left\{\begin{array}{l}{y=x-2}\\{y=-\frac{1}{2}{x}^{2}+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-4}\\{y=-6}\end{array}\right.$,
∴点P坐标为(-4,-6).
点评 本题考查考查二次函数的综合题、待定系数法、全等三角形的判定和性质、一次函数等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,利用数形结合的思想思考问题,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | (-x)2(x+y)=-x3-x2y | B. | x3+x2y=(-x)2(x+y) | C. | -x(x+y)=-x2+xy | D. | -x(x-y)=-x2-xy |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 如图1,展开后测得∠1=∠2 | B. | 如图2,展开后测得∠1=∠2且∠3=∠4 | ||
| C. | 如图3,测得∠1=∠2 | D. | 在图④中,展开后测得∠1+∠2=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,G为CD延长线上一点,连接BG交AD、AC于点E、F,若S△AEF=1,S△AFB=3,则S△GDE的值为( )
如图,在?ABCD中,G为CD延长线上一点,连接BG交AD、AC于点E、F,若S△AEF=1,S△AFB=3,则S△GDE的值为( )| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于M,交DC于N,设AE=x,则图中阴影部分的面积S与x的大致图象是( )
如图,四边形ABCD为正方形,若AB=4,E是AD边上一点(点E与点A、D不重合),BE的中垂线交AB于M,交DC于N,设AE=x,则图中阴影部分的面积S与x的大致图象是( )| A. | 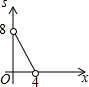 | B. | 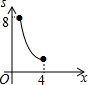 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将边长为a的正方形ABCD与边长为b的正方形ECGF(CE<AB)拼接在一起,使B、C、G三点在同一条直线上,CE在边CD上,连接AF,M为AF的中点,连接DM、CM,若ab=20,则图中阴影部分的面积为$\frac{1}{4}$a2+5.
如图,将边长为a的正方形ABCD与边长为b的正方形ECGF(CE<AB)拼接在一起,使B、C、G三点在同一条直线上,CE在边CD上,连接AF,M为AF的中点,连接DM、CM,若ab=20,则图中阴影部分的面积为$\frac{1}{4}$a2+5.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,m),C(4,m+6),那么图象同时经过点B与点D的反比例函数表达式为y=$\frac{8}{x}$.
如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为(1,m),C(4,m+6),那么图象同时经过点B与点D的反比例函数表达式为y=$\frac{8}{x}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com