
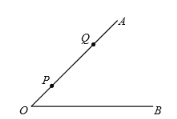
【题目】如图,![]() ,点
,点![]() 、
、![]() 都在射线
都在射线![]() 上,
上,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上的一个动点,过
上的一个动点,过![]() 、
、![]() 、
、![]() 三点作圆,当该圆与
三点作圆,当该圆与![]() 相切时,其半径的长为__________.
相切时,其半径的长为__________.
【答案】![]()
【解析】
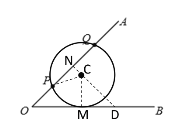
圆C过点P、Q,且与![]() 相切于点M,连接CM,CP,过点C作CN⊥PQ于N并反向延长,交OB于D,根据等腰直角三角形的性质和垂径定理,即可求出ON、ND、PN,设圆C的半径为r,再根据等腰直角三角形的性质即可用r表示出CD、NC,最后根据勾股定理列方程即可求出r.
相切于点M,连接CM,CP,过点C作CN⊥PQ于N并反向延长,交OB于D,根据等腰直角三角形的性质和垂径定理,即可求出ON、ND、PN,设圆C的半径为r,再根据等腰直角三角形的性质即可用r表示出CD、NC,最后根据勾股定理列方程即可求出r.
解:如图所示,圆C过点P、Q,且与![]() 相切于点M,连接CM,CP,过点C作CN⊥PQ于N并反向延长,交OB于D
相切于点M,连接CM,CP,过点C作CN⊥PQ于N并反向延长,交OB于D
∵![]() ,
,![]() ,
,
∴PQ=OQ-OP=4
根据垂径定理,PN=![]()
∴ON=PN+OP=4
在Rt△OND中,∠O=45°
∴ON=ND=4,∠NDO=∠O=45°,OD=![]()
设圆C的半径为r,即CM=CP=r
∵圆C与![]() 相切于点M,
相切于点M,
∴∠CMD=90°
∴△CMD为等腰直角三角形
∴CM=DM=r,CD=![]()
∴NC=ND-CD=4-![]()
根据勾股定理可得:NC2+PN2=CP2
即![]()
解得:![]() (此时DM>OD,点M不在射线OB上,故舍去)
(此时DM>OD,点M不在射线OB上,故舍去)
故答案为:![]() .
.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
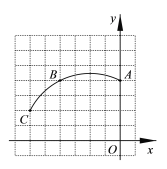
(1)利用网格图确定该圆弧所在圆的圆心D的位置(保留画图痕迹);
(2)连接AD、CD,则⊙D的半径为_ __(结果保留根号),∠ADC的度数为_ __;
(3)若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师和同学们做一个游戏:他在三张硬纸片上分别写出一个代数式,背面分别标上序号①、②、③,摆成如图所示的一个等式,然后翻开纸片②是4x2+5x+6,翻开纸片③是3x2﹣x﹣2.
![]()
解答下列问题
(1)求纸片①上的代数式;
(2)若x是方程2x=﹣x﹣9的解,求纸片①上代数式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】时代天街某商场经营的某品牌书包,6月份的销售额为20000元,7月份因为厂家提高了出厂价,商场把该品牌书包售价上涨20%,结果销量减少50个,使得销售额减少了2000元.
(1)求6月份该品牌书包的销售单价;
(2)若6月份销售该品牌书包获利8000元,8月份商场为迎接中小学开学做促销活动,该书包在6月售价的基础上一律打八折销售,若成本上涨5%,则销量至少为多少个,才能保证8月份的利润比6月份的利润至少增长6.25%?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温![]() (℃)与开机后用时
(℃)与开机后用时![]() (
(![]() )成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温
)成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温![]() (℃)与时间
(℃)与时间![]() (
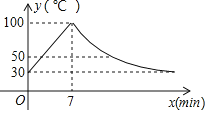
(![]() )的关系如图所示:
)的关系如图所示:
(1)分别写出水温上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学概念
若点![]() 在
在![]() 的内部,且
的内部,且![]() 、
、![]() 和
和![]() 中有两个角相等,则称
中有两个角相等,则称![]() 是
是![]() 的“等角点”,特别地,若这三个角都相等,则称
的“等角点”,特别地,若这三个角都相等,则称![]() 是
是![]() 的“强等角点”.
的“强等角点”.
理解概念
(1)若点![]() 是
是![]() 的等角点,且
的等角点,且![]() ,则
,则![]() 的度数是
的度数是 ![]() .
.
(2)已知点![]() 在
在![]() 的外部,且与点
的外部,且与点![]() 在
在![]() 的异侧,并满足
的异侧,并满足![]() ,作
,作![]() 的外接圆
的外接圆![]() ,连接
,连接![]() ,交圆
,交圆![]() 于点
于点![]() .当
.当![]() 的边满足下面的条件时,求证:
的边满足下面的条件时,求证:![]() 是
是![]() 的等角点.(要求:只选择其中一道题进行证明!)
的等角点.(要求:只选择其中一道题进行证明!)
①如图①,![]()
②如图②,![]()
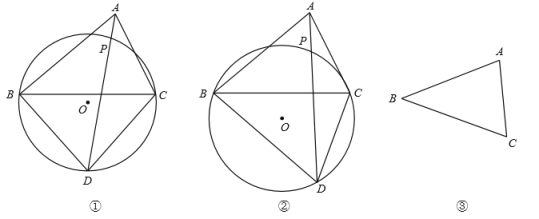
深入思考
(3)如图③,在![]() 中,
中,![]() 、
、![]() 、
、![]() 均小于
均小于![]() ,用直尺和圆规作它的强等角点
,用直尺和圆规作它的强等角点![]() .(不写作法,保留作图痕迹)
.(不写作法,保留作图痕迹)
(4)下列关于“等角点”、“强等角点”的说法:
①直角三角形的内心是它的等角点;
②等腰三角形的内心和外心都是它的等角点;
③正三角形的中心是它的强等角点;
④若一个三角形存在强等角点,则该点到三角形三个顶点的距离相等;
⑤若一个三角形存在强等角点,则该点是三角形内部到三个顶点距离之和最小的点,其中正确的有 .(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
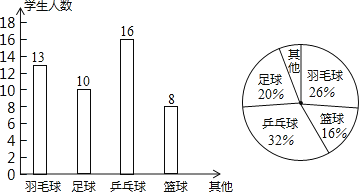
【题目】某校为了组织一次球类对抗赛,在本校随机抽取了若干名学生,对他们每个人最喜欢的一项球类运动进行了统计,将调查结果整理后绘制成如图所示的不完整的统计图,请你依据以上的信息回答下列问题:
(1)求本次被调查的学生人数;
(2)通过计算补全条形统计图;
(3)若全校有4000名学生,请你估计该校最喜欢篮球和足球运动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
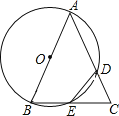
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
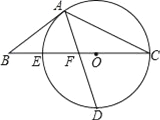
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com