
【题目】如图,在⊙O中,![]() =
=![]() ,∠ACB=60°.
,∠ACB=60°.
(1)求证:∠AOB=∠BOC=∠AOC;
(2)若点D是![]() 的中点,求证:四边形OADB是菱形.
的中点,求证:四边形OADB是菱形.

【答案】(1)见解析;(2)见解析
【解析】
(1)根据圆心角、弧、弦的关系,由![]() 得AB=AC,加上∠ACB=60°,则可判断△ABC是等边三角形,所以AB=BC=CA,于是根据圆心角、弧、弦的关系即可得到∠AOB=∠BOC=∠AOC;
得AB=AC,加上∠ACB=60°,则可判断△ABC是等边三角形,所以AB=BC=CA,于是根据圆心角、弧、弦的关系即可得到∠AOB=∠BOC=∠AOC;
(2)连接OD,如图,由D是![]() 的中点得
的中点得![]() ,则根据圆周角定理得∠AOD=∠BOD=∠ACB=60°,易得△OAD和△OBD都是等边三角形,则OA=AD=OD,OB=BD=OD,所以OA=AD=DB=BO,于是可判断四边形OADB是菱形.
,则根据圆周角定理得∠AOD=∠BOD=∠ACB=60°,易得△OAD和△OBD都是等边三角形,则OA=AD=OD,OB=BD=OD,所以OA=AD=DB=BO,于是可判断四边形OADB是菱形.
(1)∵![]() ,
,
∴AB=AC,△ABC是等腰三角形,
又∠ACB=60°,
∴△ABC是等边三角形,AB=BC=CA,
∴∠AOB=∠BOC=∠AOC;
(2)如图,连接OD,
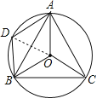
∵D是![]() 的中点,
的中点,
∴ ![]() .
.
∴∠AOD=∠BOD=![]() ∠AOB=∠ACB=60°,
∠AOB=∠ACB=60°,
又OD=OA,OD=OB,
∴△OAD和△OBD都是等边三角形,
∴OA=AD=OD,OB=BD=OD,
∴OA=AD=DB=BO,
∴四边形OADB是菱形.


科目:初中数学 来源: 题型:
【题目】如图一块直角三角形ABC,∠B=90°,AB=3,BC=4,截得两个正方形DEFG,BHJN,设S1=DEFG的面积,S2=BHJN的面积,则S1、S2的大小关系是( )
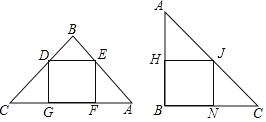
A.S1>S2B.S1<S2C.S1=S2D.不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
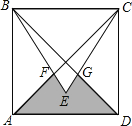
【题目】小芳参加图书馆标志设计大赛,他在边长为2的正方形ABCD内作等边△BCE,并与正方形的对角线交于F、G点,制成了图中阴影部分的标志,则这个标志AFEGD的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②3a+c>0;
③方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
④当y>3时,x的取值范围是0≤x<2;
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是二次函数y=ax2+bx+c的x,y的部分对应值:
x | … |
| 0 |
| 1 |
| 2 |
| … |
y | … |
| ﹣1 |
| m |
| ﹣1 | n | … |
则对于该函数的性质的判断:①该二次函数有最大值;②不等式y>﹣1的解集是x<0或x>2;③方程ax2+bx+c=0的两个实数根分别位于﹣![]() <x<0和2<x<
<x<0和2<x<![]() 之间;④当x>0时,函数值y随x的增大而增大;其中正确的是( )
之间;④当x>0时,函数值y随x的增大而增大;其中正确的是( )
A.②③B.②④C.①③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,4),B(4,4),C(6,0).
(1)△ABC的面积是 .
(2)请以原点O为位似中心,画出△A'B'C',使它与△ABC的相似比为1:2,变换后点A、B的对应点分别为点A'、B',点B'在第一象限;
(3)若P(a,b)为线段BC上的任一点,则变换后点P的对应点P' 的坐标为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com