
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
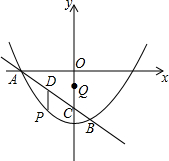 如图,已知抛物线y=ax2+c与直线$y=-\frac{3}{4}x-3$交于A,B两点,直线AB与y轴交于点C,点B的坐标为(1,$-\frac{15}{4}$),动点P在直线AB下方的抛物线上,动点Q在y轴上,动点D在线段AB上,且PD∥y轴.
如图,已知抛物线y=ax2+c与直线$y=-\frac{3}{4}x-3$交于A,B两点,直线AB与y轴交于点C,点B的坐标为(1,$-\frac{15}{4}$),动点P在直线AB下方的抛物线上,动点Q在y轴上,动点D在线段AB上,且PD∥y轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
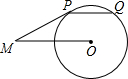 如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )
如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
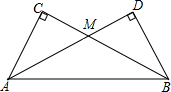 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查全国中学生心理健康现状 | |
| B. | 调查我市食品合格情况 | |
| C. | 调查你所在的班级同学的身高情况 | |
| D. | 调查桂林电视台某电视节目的收视率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com