
 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
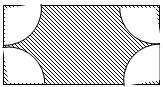 如图是某居民小区的一块长为b米,宽为2a米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?
如图是某居民小区的一块长为b米,宽为2a米的长方形空地,为了美化环境,准备在这个长方形的四个顶点处修建一个半径为a米的扇形花台,然后在花台内种花,其余种草.如果建造花台及种花费用每平方米需要资金100元,种草每平方米需要资金50元,那么美化这块空地共需资金多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
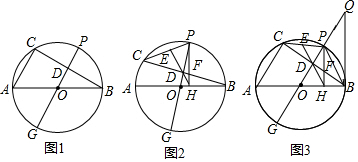
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com