练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某次列车平均提速，用相同的时间，列车提速前行驶，提速后比提速前多行驶，提速前列车的平均速度为多少？若设提速前这次列车的平均速度为，则根据行驶时间的等量关系可以列出的方程为（ ）

    A. B. C. D.

    【答案】A

    【解析】

    首先根据题意找到等量关系，时间=路程÷速度，用列车提速前行驶的路程除以提速前的速度，求出列车提速前行驶skm用的时间是多少；然后用列车提速后行驶的路程除以提速后的速度，求出列车提速后行驶s+50km用的时间是多少；最后根据列车提速前行驶skm和列车提速后行驶s+50km时间相同，列出方程即可．

    解：列车提速前行驶skm用的时间是小时，
    列车提速后行驶s+50km用的时间是小时，
    因为列车提速前行驶skm和列车提速后行驶s+50km时间相同，
    所以列方程是

    ．
    故选：A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知反比例函数y= 的图象如图所示，则二次函数y=﹣kx2﹣2x+ 的图象大致为（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据： ≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公园有一个抛物线形状的观景拱桥ABC，其横截面如图所示，在图中建立的直角坐标系中，抛物线的解析式为y=﹣ +c且过顶点C（0，5）（长度单位：m）

    （1）直接写出c的值；
    （2）现因搞庆典活动，计划沿拱桥的台阶表面铺设一条宽度为1.5m的地毯，地毯的价格为20元/m2 ， 求购买地毯需多少元？
    （3）在拱桥加固维修时，搭建的“脚手架”为矩形EFGH（H、G分别在抛物线的左右侧上），并铺设斜面EG．已知矩形EFGH的周长为27.5m，求斜面EG的倾斜角∠GEF的度数．（精确到0.1°）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在正方形ABCD中,E、F分别为BC、CD的中点,AE与BF相交于点G．

    （1）如图1,求证：AE⊥BF；

    （2）如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将正方形对折后展开（图④是连续两次对折后再展开），再按图示方法折叠，能够得到一个直角三角形（阴影部分），且它的一条直角边等于斜边的一半．这样的图形有（ ）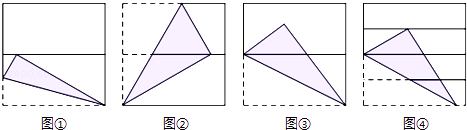

    A.4个
    B.3个
    C.2个
    D.1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们已经知道，有一个内角是直角的三角形.其中直角所在的两条边叫直角边，直角所对的边叫斜边.数学家已发现在一个直角三角形中，两条直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是和，斜边长度是，那么可以用数学语言表达为：.

    （1）在图中，若，，则等于多少；

    （2）观察图，利用面积与代数恒等式的关系，试说明的正确性.其中两个相同的直角三角形边、在一条直线上；

    （3）如图③所示，折叠长方形的一边，使点落在边的点处，已知，，利用上面的结论求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点 O是△ABC外接圆的圆心，若⊙O的半径为5，∠A=45°，则 的长是（ ）

    A. π
    B. π
    C. π
    D. π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于正整数m，若m=pq（p≥q＞0，且p，q为整数），当p-q最小时，则称pq为m的“最佳分解”，并规定f（m）=（如：12的分解有12×1，6×2，4×3，其中，4×3为12的最佳分解，则f（12）=）．关于f（m）有下列判断：①f（27）=3；②f（13）=；③f（2018）=；④f（2）=f（32）．其中，正确判断的序号是______．

    查看答案和解析>>

    同步练习册答案