
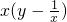 ,其中x,y为正整数,求x+y的最大值和最小值.
,其中x,y为正整数,求x+y的最大值和最小值.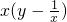
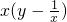 可知xy=2009,再根据x,y为正整数,确定x、y可能的取值.根据xy的乘积的个位是9,确定x、y的个位可能是1、3、7、9.通过x、y都具有同等的地位,那么x取过的值,y也有可能,故只取x即可,x的十位数最大不会超过5.因而
可知xy=2009,再根据x,y为正整数,确定x、y可能的取值.根据xy的乘积的个位是9,确定x、y的个位可能是1、3、7、9.通过x、y都具有同等的地位,那么x取过的值,y也有可能,故只取x即可,x的十位数最大不会超过5.因而

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
| 型号 | A | B |
| 进价(元/台) | 2000 | 2400 |
| 售价(元/台) | 2500 | 3000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 5020 |
| 1+12.8% |
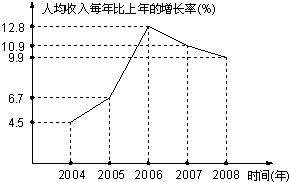
| A、①③ | B、②③ | C、①②④ | D、②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:
. |
| 新北京 |
. |
| 新北 |
| 1 |
| 新 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com