
【题目】如图,已知PA、PB是⊙O的切线,A、B分别为切点,∠OAB=30°.
(1)∠APB=_____;
(2)当OA=2时,AP=_____.

【答案】60° 2![]() .
.
【解析】
(1)根据四边形的内角和为360°,根据切线的性质可知:∠OAP=∠OBP=90°,求出∠AOB的度数,可将∠APB的度数求出;
(2)作辅助线,连接OP,在Rt△OAP中,利用三角函数,即可求出AP的长
(1)∵在△ABO中,OA=OB,∠OAB=30°,
∴∠AOB=180°﹣2×30°=120°,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,即∠OAP=∠OBP=90°,
∴在四边形OAPB中,
∠APB=360°﹣120°﹣90°﹣90°=60°,
故答案为:60°.
(2)如图,连接OP;
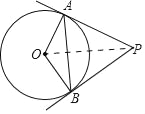
∵PA、PB是⊙O的切线,
∴PO平分∠APB,即∠APO=![]() ∠APB=30°,
∠APB=30°,
又∵在Rt△OAP中,OA=3,∠APO=30°,
∴AP=![]() =
=![]() = 2
= 2![]()
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
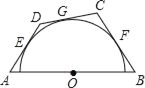
【题目】如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF,在![]() 上取动点G,国点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
上取动点G,国点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
A. 正比例函数y=kx(k为常数,k≠0,x>0)
B. 一次函数y=kx+b(k,b为常数,kb≠0,x>0)
C. 反比例函数y=![]() (k为常数,k≠0,x>0)
(k为常数,k≠0,x>0)
D. 二次函数y=ax2+bx+c(a,b,c为常数,a≠0,x>0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何模型:
条件:如图1,A、B是直线![]() 同旁的两个定点.
同旁的两个定点.

问题:在直线![]() 上确定一点P,使PA+PB的值最小.
上确定一点P,使PA+PB的值最小.
方法:作点A关于直线![]() 的对称点A′,连接A′B交
的对称点A′,连接A′B交![]() 于点P,则PA+PB=A′B的值最小(不必证明).
于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
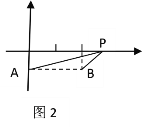
(1)如图2,已知平面直角坐标系中两定点A(0,-1),B(2,-1),P为x轴上一动点, 则当PA+PB的值最小时,点P的横坐标是______,此时PA+PB的最小值是______;
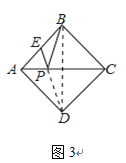
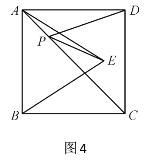
(2)如图3,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.由正方形对称性可知,B与D关于直线AC对称,连接BD,则PB+PE的最小值是______;
(3)如图4,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,则PD+PE的最小值为 ;
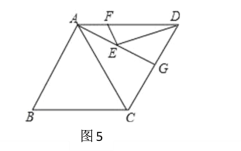
(4)如图5,在菱形ABCD中,AB=8,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上, ΔAEF是等边三角形,连接AC交EF于点G,下列结论:①CE=CF,②∠AEB=75°,③AG=2GC,④BE+DF=EF,⑤S△CEF=2S△ABE,其中结论正确的个数为( )
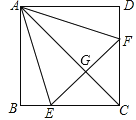
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知平行四边形ABCD,对角线AC,BD相交于点O,∠OBC=∠OCB.
(1)求证:平行四边形ABCD是矩形;
(2)请添加一个条件使矩形ABCD为正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
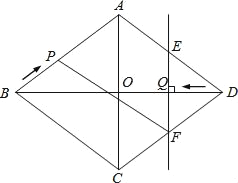
【题目】如图,在菱形ABCD中,AC,BD交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为lcm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为lcm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q.F,当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)求菱形ABCD的面积;
(2)当t=1时,求QF长;
(3)是否存在某一时刻t,使四边形APFD是平行四边形?若存在,求出t值,若不存在,请说明理由;
(4)设△DEF的面积为s(cm2),试用含t的代数式表示S,并求t为何值时,△DEF的面积与△BPC的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
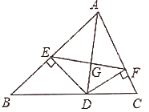
【题目】如图,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的高,连接
的高,连接![]() 交
交![]() 于
于![]() .下列结论:①
.下列结论:①![]() 垂直平分
垂直平分![]() ;②
;②![]() 垂直平分
垂直平分![]() ;③
;③![]() 平分
平分![]() ;④当
;④当![]() 为
为![]() 时,
时,![]() ,其中不正确的结论的个数为( )
,其中不正确的结论的个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com