【题目】解方程
（1）（x-2）（x+3）=-4 （公式法） （2）2x2+4x+1=25（配方法）
（3）3（x-5）2=x-5 （4）（x+3）2=（3x-5）2．
【答案】（1）x1=-2，x2=1；（2）x1=-1+
，x2=-1-；（3）x1=5，x2=
；（4）x1=4，x2=
．
【解析】试题分析：（1）先化简（x-2）（x+3）=-4后，再用公式法解方程即可；（2）先将2x2+4x+1=25变形成x2+2x-12=0，再根据完全平方和公式配方，再直接开平方即可；（3）先移项，再提取公因式，再令因式为0，求得x的值即可；（4）直接开平方求得x的值即可；
试题解析：
解：（1）x2+x-2=0，
（x+2）（x-1）=0，
x+2=0或x-1=0，
所以x1=-2，x2=1；
（2）x2+2x-12=0，
x2+2x+1=13，
（x+1）2=13，
x+1=±，
所以x1=-1+，x2=-1-；
（3）3（x-5）2-（x-5）=0，
（x-5）（3x-15-1）=0，
x-5=0或3x-15-1=0，
所以x1=5，x2= ；
（4）x+3=±（3x-5），
所以x1=4，x2=．
一课一练课时达标系列答案科目：初中数学 来源： 题型：
【题目】（1）观察一列数a1=3，a2=9，a3=27，a4=81，…，发现从第二项开始，每一项与前一项之比是一个常数，这个常数是 ；根据此规律，如果an（n为正整数）表示这个数列的第n项，那么a
= ，a
= ；（可用幂的形 式表示）
（2）如果想要求1+2+22+2
+…+2
的值，
可令S10=1+2+22+2
+…+2
①
将①式两边同乘以2，得2S10= ，②
由②式减去①式，得S10= .
（3）有一组数列，其中a1=1,a2=3,a3=9……an=3n-1，
请利用上述规律和方法计算a21+a22+a23+……a30的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若△ABC 的边长为 a、b、c，且满足 a2+b2+c2＝ab+bc+ca，则△ABC 的形状是（ ）
A.等腰三角形B.等边三角形C.任意三角形D.不能确定
查看答案和解析>>
科目：初中数学 来源： 题型：
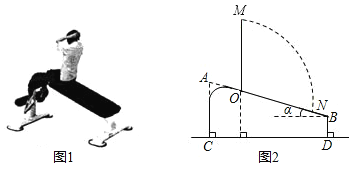
【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景，图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图．已知AC=0.66米，BD=0.26米，α=20°．（参考数据：sin20°≈0.342，cos20°≈0.940，tan20°≈0.364）
（1）求AB的长（精确到0.01米）；
（2）若测得ON=0.8米，试计算小明头顶由N点运动到M点的路径
的长度．（结果保留π）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，P是等边三角形ABC内的一点，且PA=3，PB=4，PC=5，以BC为边在△ABC外作△BQC≌△BPA，连接PQ，则以下结论错误的是（ ）
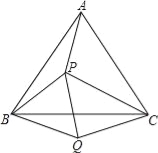
A．△BPQ是等边三角形
B．△PCQ是直角三角形
C．∠APB=150°
D．∠APC=135°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
