
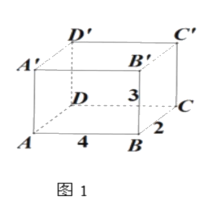
【题目】如图1是长方体模型,棱长如图所示,图2是它的一种表面展开图.
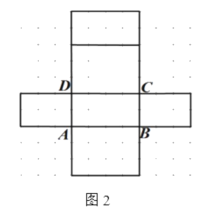

(1)①在图2中,表示出C可能的位置;
②在图3中画出长方体的一种展开图(不同于图2);
(2)图1中,一只在顶点A的蚂蚁,要吃到C处的甜食,求它沿长方体表面爬行的最短距离;
(3) 在满足AB+BC+BB=9的条件下,当AB为何值时,蚂蚁从A沿长方体表面爬行到C距离最短,并写出其中的一种方案.
【答案】(1)①详见解析;②详见解析;(2)最短路径为![]() ;(3)AB=4.5时,蚂蚁从A沿长方体表面爬行到C距离最短
;(3)AB=4.5时,蚂蚁从A沿长方体表面爬行到C距离最短
【解析】
(1)①根据长方体的平面展开图即可找到位置;
②根据题意画出正确的图形即可;
(2)连接AC′,求出AC′的长即可,分为三种情况:画出图形,根据勾股定理求出每种情况时AC′的长,再找出最短的即可;
(3)设AB=x,则BC′=![]() ,由勾股定理构建二次函数,根据二次函数的最值,即可求得答案.
,由勾股定理构建二次函数,根据二次函数的最值,即可求得答案.
(1)①C可能的位置如图所示:
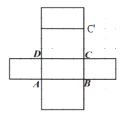
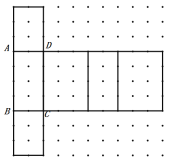
②长方体的一种展开图如图所示:
(2)分为三种情况:
如图1,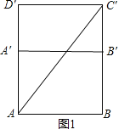
AB=4,BC′=3+2=5,
在Rt△ABC′中,由勾股定理得:
![]() ,
,
如图2,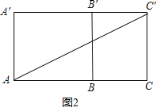
AC=4+2=6,CC′=3,
在Rt△ACC′中,由勾股定理得:
![]() ,
,
如图3,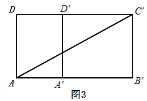
![]() =3+4=7,
=3+4=7,![]() C′=2,
C′=2,
在![]() ′中,由勾股定理得:
′中,由勾股定理得:
![]() ,
,
∴最短路径为![]() ;
;
(3)如图1:

设![]() ,则BC′=
,则BC′=![]() ,
,
在Rt△ABC′中,由勾股定理得:
![]() ,
,
d=![]() ,
,
令y=2(x-![]() )
)![]() +
+![]() ,
,
∵![]() 且
且![]() ,
,
∴当![]()
![]() 时,
时,![]() ,
,
∴当![]()
![]() 时,
时,![]() .
.
只要AB=4.5时,另外两棱和为4.5时,蚂蚁从A沿长方体表面爬行到C距离最短.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】某农科所研究出一种新型的花生摘果设备,一期研发成本为每台6万元,该摘果机的销售量![]() (台)与售价
(台)与售价![]() (万元/台)之间存在函数关系:
(万元/台)之间存在函数关系:![]() .
.
(1)设这种摘果机一期销售的利润为![]() (万元),问一期销售时,在抢占市场份额(提示:销量尽可能大)的前提下利润达到32万元,此时售价为多少?
(万元),问一期销售时,在抢占市场份额(提示:销量尽可能大)的前提下利润达到32万元,此时售价为多少?
(2)由于环保局要求该机器必须增加除尘设备,科研所投入了7万元研究经费,使得环保达标且机器的研发成本每台降低了1万元,若科研所的销售战略保持不变,请问在二期销售中利润达到63万元时,该机器单台的售价为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
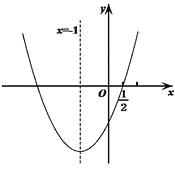
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列5个结论:①
,下列5个结论:①![]() ; ②
; ②![]() ; ③
; ③![]() ;④
;④![]() ; ⑤
; ⑤![]() ,其中正确的结论为________________.(注:只填写正确结论的序号)
,其中正确的结论为________________.(注:只填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
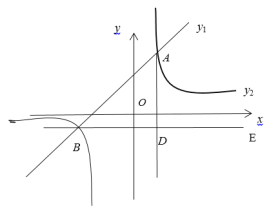
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b的图像与反比例函数![]() 的图像交于点A(2,4)和B(-4,m).
的图像交于点A(2,4)和B(-4,m).
(1)求一次函数和反比例函数的表达式;
(2)过点B做BE//x轴,![]() 于点D,点C是直线BE上一点,若AC=2BC,求点C的坐标.
于点D,点C是直线BE上一点,若AC=2BC,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中点A的坐标为(3,6),点B(6,0),C是线段OB上一动点(不与O,B重合),过C,O两点的二次函数y1和过C,B两点的二次函数y2的图像开口均向下,它们的顶点分别为OA,AB边上的E,F两点,点C从点O到点B运动过程中,阴影部分的面积大小变化情况是( )
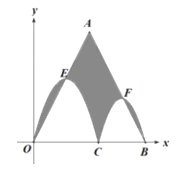
A.不变B.先增大再减小C.先减小再增大D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 、正方形
、正方形![]() 如图放置,点
如图放置,点![]() 在同一条直线上,点
在同一条直线上,点![]() 在
在![]() 边上,
边上,![]() ,且
,且![]() ,连结
,连结![]() 交
交![]() 于
于![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .以上结论正确的个数有( )
.以上结论正确的个数有( )
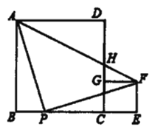
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,垂足为点
,垂足为点![]() .则以下结论:①
.则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,⑤
,⑤![]() ,其中正确的结论有( )
,其中正确的结论有( )
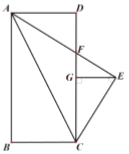
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com