
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥OC
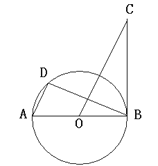
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=![]() ,求AD的长(结果保留根号).
,求AD的长(结果保留根号).
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】类比、转化等数学思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
已知![]() .
.
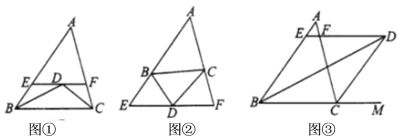
(1)观察发现
如图①,若点![]() 是
是![]() 和
和![]() 的角平分线的交点,过点
的角平分线的交点,过点![]() 作
作![]() 分别交
分别交![]() 、
、![]() 于、
于、![]() ,
,![]() 填空:
填空: ![]() 与
与![]() 、
、![]() 的数量关系是________________________________________.
的数量关系是________________________________________.
(2)猜想论证
如图②,若![]() 点是外角
点是外角![]() 和
和![]() 的角平分线的交点,其他条件不变,填:
的角平分线的交点,其他条件不变,填: ![]() 与
与![]() 、
、![]() 的数量关系是_____________________________________.
的数量关系是_____________________________________.
(3)类比探究
如图③,若点![]() 是
是![]() 和外角
和外角![]() 的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
的角平分线的交点.其他条件不变,则(1)中的关系成立吗?若成立,请加以证明;若不成立,请写出关系式,再证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
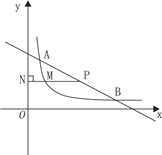
【题目】如图,直线![]() 与双曲线
与双曲线![]() 交于A,B两点,A点的横坐标为2.
交于A,B两点,A点的横坐标为2.
(1)求点B的坐标;
(2)P为线段AB上一点(不包括端点),P点的纵坐标为a,作PN⊥y轴,垂足为N,交双曲线于点M,求![]() 的最大值;
的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:用若干个边长为1的小等边三角形拼成![]() 层的大等边三角形,共需要多少个小等边三角形?共有线段多少条?
层的大等边三角形,共需要多少个小等边三角形?共有线段多少条?
图① 图②
图② 图③
图③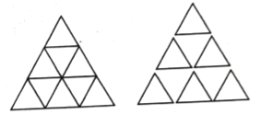
问题探究:
如图①,是一个边长为1的等边三角形,现在用若干个这样的等边三角形再拼成更大的等边三角形.
(1)用图①拼成两层的大等边三角形,如图②,从上往下,第一层有1个,第二层有2个,共用了![]() 个图①的等边三角形,则有长度为1的线段
个图①的等边三角形,则有长度为1的线段![]() 条;还有边长为2的等边三角形1个,则有长度为2的线段
条;还有边长为2的等边三角形1个,则有长度为2的线段![]() 条;所以,共有线段
条;所以,共有线段![]() 条.
条.
(2)用图①拼成三层的大等边三角形,如图③,从上往下,第一层有1个,第二层有2个,第三层有3个,共用了![]() 个图①的等边三角形,则有长度为1的线段
个图①的等边三角形,则有长度为1的线段![]() 条;还有边长为2的等边三角形
条;还有边长为2的等边三角形![]() 个,则有长度为2的线段
个,则有长度为2的线段![]() 条;还有边长为3的等边三角形1个,则有长度为3的线段
条;还有边长为3的等边三角形1个,则有长度为3的线段![]() 条;所以,共有线段
条;所以,共有线段![]() 条.……
条.……
问题解决:
(3)用图①拼成四层的大等边三角形,共需要多少个图①三角形?共有线段多少条?请在方框中画出一个示意图,并写出探究过程;
(4)用图①拼成20层的大等边三角形,共用了 个图①三角形,共有线段 条;
(5)用图①拼成![]() 层的大等边三角形,共用了 个图①三角形,共有线段 条,其中边长为2的等边三角形共有 个.
层的大等边三角形,共用了 个图①三角形,共有线段 条,其中边长为2的等边三角形共有 个.
(6)拓展提升:如果用边长为3的小等边三角形拼成边长为30的大等边三角形,共需要 个小等边三角形,共有线段 条.
查看答案和解析>>
科目:初中数学 来源: 题型:
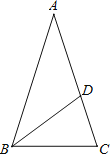
【题目】如图,等腰△ABC中,AB=AC,∠BAC=36°,BC=1,点D在边AC上且BD平分∠ABC,设CD=x.
(1)求证:△ABC∽△BCD;
(2)求x的值;
(3)求cos36°-cos72°的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果∠α和∠β互补,且∠α<∠β,则下列表示∠α的余角的式子中:①90°﹣∠α;②∠β﹣90°;③![]() (∠α+∠β);④
(∠α+∠β);④![]() (∠β﹣∠α)其中正确的有( )
(∠β﹣∠α)其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知线段![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点
上的一个动点![]() ,点
,点![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

(1)若点![]() 恰好是
恰好是![]() 的中点,则
的中点,则![]() _______
_______![]() ;若
;若![]() ,则
,则![]() _________
_________![]() ;
;
(2)随着点![]() 位置的改版,
位置的改版,![]() 的长是否会改变?如果改变,请说明原因;如果不变,请求出的长;
的长是否会改变?如果改变,请说明原因;如果不变,请求出的长;
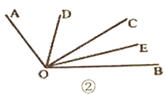
(3)知识迁移:如图②,已知![]() ,过角的内部任意一点
,过角的内部任意一点![]() 画射线
画射线![]() ,若
,若![]() 分别平分
分别平分![]() 和
和![]() ,试说明
,试说明![]() 的度数与射线
的度数与射线![]() 的位置无关.
的位置无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
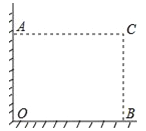
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计算:当用水量不超过![]() 吨时,每吨的收费标准相同,当用水量超过
吨时,每吨的收费标准相同,当用水量超过![]() 吨时,超出
吨时,超出![]() 吨的部分每吨的收费标准也相同,下表是小明家
吨的部分每吨的收费标准也相同,下表是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
用水量(吨) |
|
|
|
|
费用(元) |
|
|
|
|
请根据表格中提供的信息,回答以下问题:
(1)若小明家![]() 月份用水量为
月份用水量为![]() 吨,则应缴水费________元;
吨,则应缴水费________元;
(2)若某户某月用了![]() 吨水(
吨水(![]() ),应付水费________元;
),应付水费________元;
(3)若小明家![]() 月份交纳水费
月份交纳水费![]() 元,则小明家
元,则小明家![]() 月份用水多少吨?
月份用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com