
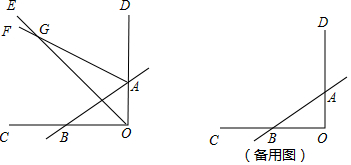
分析 (1)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,再根据三角形外角性质进行计算即可;
(2)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,再根据三角形外角性质进行计算即可;
(3)根据三角形外角的性质求出∠BAD,求出∠GOA和∠GAD,再根据三角形外角性质进行计算即可;
(4)分两种讨论:∠EOD:∠COE=1:2,∠EOD:∠COE=2:1,分别运用上述方法即可得到∠OGA的度数.
解答 解:(1)∵∠BOA=90°,∠OBA=42°,
∴∠BAD=∠BOA+∠ABO=132°,
∵AF平分∠BAD,OE平分∠BOA,∠BOA=90°,
∴∠GAD=$\frac{1}{2}$∠BAD=66°,∠EOA=$\frac{1}{2}$∠BOA=45°,
∴∠OGA=∠GAD-∠EOA=66°-45°=21°;
故答案为:21°;
(2)∵∠BOA=90°,∠OBA=42°,
∴∠BAD=∠BOA+∠ABO=132°,
∵∠BOA=90°,∠GOA=$\frac{1}{3}$∠BOA,∠GAD=$\frac{1}{3}$∠BAD,
∴∠GAD=44°,∠EOA=30°,
∴∠OGA=∠GAD-∠EOA=44°-30°=14°;
故答案为14°;
(3)∵∠BOA=90°,∠OBA=α,
∴∠BAD=∠BOA+∠ABO=90°+α,
∵∠BOA=90°,∠GOA=$\frac{1}{3}$∠BOA,∠GAD=$\frac{1}{3}$∠BAD,
∴∠GAD=30°+$\frac{1}{3}$α,∠EOA=30°,
∴∠OGA=∠GAD-∠EOA=$\frac{1}{3}$α;
(4)当∠EOD:∠COE=1:2时,∠EOD=30°,
∵∠BAD=∠ABO+∠BOA=α+90°,而AF平分∠BAD,
∴∠FAD=$\frac{1}{2}$∠BAD=$\frac{1}{2}$(α+90°),
∵∠FAD=∠EOD+∠OGA,
∴30°+∠OGA=$\frac{1}{2}$(α+90°),
解得∠OGA=$\frac{1}{2}$α+15°;
当∠EOD:∠COE=2:1时,∠EOD=60°,
同理可得∠OGA=$\frac{1}{2}$α-15°;
综上所述,∠OGA的度数为$\frac{1}{2}$α+15°或$\frac{1}{2}$α-15°.
点评 本题考查了三角形内角和定理,角平分线的定义以及三角形外角性质.解题时注意:三角形内角和为180°,三角形的外角等于与它不相邻的两个内角的和.


科目:初中数学 来源: 题型:解答题
| 摸球次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 |
| 摸出红球的频数 | 14 | 23 | 38 | 52 | 67 | 80 | 93 |
| 摸出红球的频率 | 35% | 28.75% | 32% | 33% | 33.55 | 33.33% | 33% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
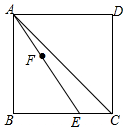 如图,在正方形ABCD中,E为BC边上一点,连结AE.已知AB=8,CE=2,F是线段AE上一动点.若BF的延长线交正方形ABCD的一边于点G,且满足AE=BG,则$\frac{BF}{FG}$的值为1或$\frac{12}{13}$.
如图,在正方形ABCD中,E为BC边上一点,连结AE.已知AB=8,CE=2,F是线段AE上一动点.若BF的延长线交正方形ABCD的一边于点G,且满足AE=BG,则$\frac{BF}{FG}$的值为1或$\frac{12}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
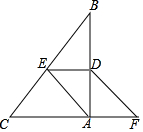 如图,在Rt△ABC中,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.
如图,在Rt△ABC中,∠BAC=90°,D,E分别为AB,BC的中点,点F在CA的延长线上,∠FDA=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
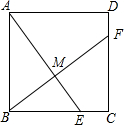 如图,已知正方形ABCD的边长为8,点EF分别是边BC、CD的点,且BE=CF=6.
如图,已知正方形ABCD的边长为8,点EF分别是边BC、CD的点,且BE=CF=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com