
【题目】如图,在⊙O中,AB为直径,AC为弦,过点C作CD⊥AB于点D,将△ACD沿AC翻折,点D落在点E处,AE交⊙O于点F,连接OC、FC.
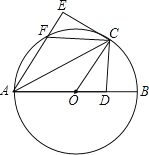
(1)求证:CE是⊙O的切线.
(2)若FC∥AB,求证:四边形AOCF是菱形.
【答案】见解析
【解析】
试题分析:(1)由翻折的性质可知∠FAC=∠OAC,∠E=∠ADC=90°,然后根据OA=OC得到∠OAC=∠OCA,从而得到OC∥AE,得到∠OCE=90°,从而判定切线.
(2)利用FC∥AB,OC∥AF判定四边形AOCF是平行四边形,根据OA=OC,利用邻边相等的平行四边形是菱形判定□AOCF是菱形.
(1)证明:由翻折可知∠FAC=∠OAC,∠E=∠ADC=90°,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC∥AE
∴∠OCE=90°,
即OC⊥CE,
∵OC是⊙O的半径
∴CE是⊙O的切线;
(2)证明:∵FC∥AB,OC∥AF,
∴四边形AOCF是平行四边形,
∵OA=OC,
∴平行四边形AOCF是菱形.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P的坐标为(-5,3),则点P关于y轴的对称
点的坐标是( )
A. (5,3) B. (-5,-3) C. (3,-5) D. (-3,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.延长射线OA到点B
B.线段AB为直线AB的一部分
C.画一条直线,使它的长度为3cm
D.射线AB和射线BA是同一条射线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=﹣![]() x+4的图象与x轴交于A,与y轴交于点B.
x+4的图象与x轴交于A,与y轴交于点B.

(1)求点A,B的坐标并在如图的坐标系中画出函数y=﹣![]() x+4的图象;
x+4的图象;
(2)若一次函数y=kx﹣2的图象经过点A,求它的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
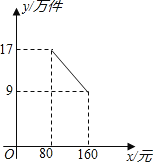
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 任意两个等腰三角形都相似 B. 任意两个菱形都相似
C. 任意两个正五边形都相似 D. 对应角相等的两个多边形相似
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com