
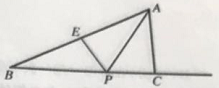
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,E为斜边AB的中点,点P是射线BC的一个动点,连接AP、PE,将△AEP沿着边PE叠,折叠后得到△EPA,当折叠后△EPA与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则BP的长__________
【答案】4或![]() .
.
【解析】分析: 根据30°角所对直角边等于斜边的一半可求出AB,即可得到AE的值,然后根据勾股定理求出BC,①若![]() 与AB交于点F,连接
与AB交于点F,连接![]() ,如图1,易得
,如图1,易得![]() ,即可得到
,即可得到![]() ,
,![]() .从而可得四边形
.从而可得四边形![]() 是平行四边形,即可得到
是平行四边形,即可得到![]() ,从而可求出BP;②若
,从而可求出BP;②若![]() 与BC交于点G,连接
与BC交于点G,连接![]() ,交EP与H,如图2,同理可得
,交EP与H,如图2,同理可得![]() ,
,![]() EG=
EG=![]() ,根据三角形中位线定理可得AP=4=AC,此时点P与点C重合
,根据三角形中位线定理可得AP=4=AC,此时点P与点C重合![]() ,从而可求出BP.
,从而可求出BP.
详解:因为Rt△ABC中,∠ACB=90°,∠A=60°,AC=4,E为斜边AB的中点,
所以AB=8,AE=4,BC=![]() ,
,
①若PA’与AB交于点F,连接A’B,如图1.
由折叠可得AE=AE’=4,.
因为点E是AB的中点,![]()
由题可得![]() ,
,![]() ,
,![]() ,
,![]()
所以四边形A’EPB是平行四边形,
所以BP=A’E=4;
②若EA’与BC交于点G,连接AA’,交EP与H,如图2. .
.
同理可得![]() ,
,
因为![]()
所以![]() ,
,
所以点P与点C重合,
所以BP=BC=![]() ,
,
故答案为4或![]()


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,﹣1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO在平面直角坐标系中,且A(1,2),B(5,4),C(6,0),O(0,0).
(1)求四边形ABCO的面积;
(2)将四边形ABCO四个顶点的横坐标都减去3,同时纵坐标都减去2,画出得到的四边形A′B′C′O′,你能从中得到什么结论?
(3)直接写出四边形A′B′C′O′的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列从左到右的变形,是因式分解的是( )
A. m2-1=(m+1)(m-1) B. 2(a-b)=2a-2b C. x2-2x+1=x(x-2)+1, D. a(a-b)(b+1)=(a2 -ab)(b+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形纸片ABCD的边长为4,将该正方形纸片沿EF折叠(E,F分别在AB,CD边上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P.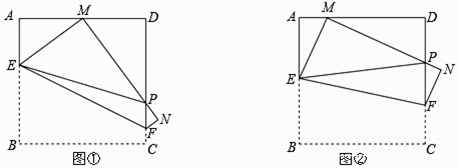
(1)如图①,连接PE,若M是AD边的中点.
①写出图中与△PMD相似的三角形.
②求△PMD的周长.
(2)如图②,随着落点M在AD边上移动(点M不与A、D重合),△PDM的周长是否发生变化?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数 ![]() 图象如图,以下结论,其中正确有( )个:
图象如图,以下结论,其中正确有( )个:
①m<0;
②在每个分支上y随x的增大而增大;
③若A(﹣1,a),点B(2,b)在图象上,则a<b
④若P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.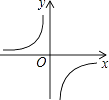
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.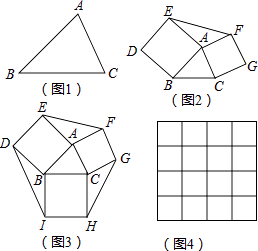
(1)图1中的△ABC的BC边上有一点D,线段AD将△ABC分成两个互补三角形,则点D在BC边的处.
(2)证明:图2中的△ABC分割成两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI,已知三个正方形面积分别是17、13、10.则图3中六边形DEFGHI的面积为 . (提示:可先利用图4求出△ABC的面积)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com