
°Њћвƒњ°њ»зЌЉ£ђ“—÷™£Ї≈„ќпѕяy£љx2+bx+c”лx÷бљї”ЏA£®©Б1£ђ0£©£ђB£®3£ђ0£©Ѕљµг£ђ”лy÷бљї”ЏµгC£ђµгDќ™ґ•µг£ђЅђљ”BD£ђCD£ђ≈„ќпѕяµƒґ‘≥∆÷б”лx÷бљї”лµгE£Ѓ
£®1£©«у≈„ќпѕяљвќц љЉ∞µгDµƒ„ш±к£ї
£®2£©G «≈„ќпѕя…ѕB£ђD÷ЃЉдµƒ“їµг£ђ«“SЋƒ±я–ќCDGB£љ4S°чDGB£ђ«у≥цGµг„ш±к£ї
£®3£©‘Џ≈„ќпѕя…ѕB£ђD÷ЃЉд «Јсіж‘Џ“їµгM£ђєэµгM„чMN°ЌCD£ђљї÷±ѕяCD”ЏµгN£ђ є“‘C£ђM£ђNќ™ґ•µгµƒ»эљ«–ќ”л°чBDEѕаЋ∆£њ»фіж‘Џ£ђ«у≥ц¬ъ„гћхЉюµƒµгMµƒ„ш±к£ђ»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£Ѓ

°Њір∞Є°њ£®1£©![]() £їґ•µг
£їґ•µг![]()
![]() £ї£®2£©
£ї£®2£©![]() £ї£®3£©іж‘Џ£ђµг
£ї£®3£©іж‘Џ£ђµг![]() їт
їт![]() £Ѓ
£Ѓ
°Њљвќц°њ
£®1£©јы”√іэґ®ѕµ эЈ®њ…«уµ√≈„ќпѕяµƒљвќц љ£ђ»їЇуїѓ≥…ґ•µг љњ…µ√µгDµƒ„ш±к£ї
£®2£©Ѕђљ”BC£ђBG£ђDG£ђ „ѕ»«у≥ц![]() £ђ»їЇуЄщЊЁSЋƒ±я–ќCDGB£љ4S°чDGBњ…µ√
£ђ»їЇуЄщЊЁSЋƒ±я–ќCDGB£љ4S°чDGBњ…µ√![]() £ђ«у≥ц÷±ѕя
£ђ«у≥ц÷±ѕя![]() µƒљвќц љ£ђ…и
µƒљвќц љ£ђ…и![]() £ђ‘тH£®x£ђ2x-6£©£ђЄщЊЁ
£ђ‘тH£®x£ђ2x-6£©£ђЄщЊЁ![]() µ√≥цЈљ≥ћ£ђљвЈљ≥ћ«у≥цxЉіњ…љвЊцќ ћв£ї
µ√≥цЈљ≥ћ£ђљвЈљ≥ћ«у≥цxЉіњ…љвЊцќ ћв£ї
£®3£©»зЌЉ3£ђ“‘C£ђM£ђNќ™ґ•µгµƒ»эљ«–ќ”л°чBDEѕаЋ∆£ђ‘т“‘B£ђC£ђPќ™ґ•µгµƒ»эљ«–ќ”л°чBDEѕаЋ∆£ђ‘т![]() їт
їт![]() £ђ«у≥ц
£ђ«у≥ц![]() їт
їт![]() £ї»їЇуЈ÷
£ї»їЇуЈ÷![]() ЇЌ
ЇЌ![]() Ѕљ÷÷«йњц£ђЈ÷±р«у≥ц÷±ѕяCPµƒљвќц љЉіњ…љвЊцќ ћв£Ѓ
Ѕљ÷÷«йњц£ђЈ÷±р«у≥ц÷±ѕяCPµƒљвќц љЉіњ…љвЊцќ ћв£Ѓ
љв£Ї£®1£©![]() ≈„ќпѕя
≈„ќпѕя![]() ”л
”л![]() ÷бљї”Џ
÷бљї”Џ![]() £ђ
£ђ![]() Ѕљµг£ђ
Ѕљµг£ђ
![]() £ђљвµ√
£ђљвµ√![]() £ђ
£ђ
°а≈„ќпѕяµƒљвќц љќ™£Ї![]() £ї
£ї
![]() £ђ
£ђ
![]() ґ•µг
ґ•µг![]() µƒ„ш±кќ™
µƒ„ш±кќ™![]() £ї
£ї
£®2£©»зЌЉ2£ђЅђљ”![]() £ђBG£ђDG£ђ
£ђBG£ђDG£ђ
‘Џ![]() ÷–£ђЅо
÷–£ђЅо![]() £ђ‘т
£ђ‘т![]() £ђ
£ђ
°аµг![]() £ђ
£ђ
°а“„«у÷±ѕя![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђ
£ђ
…и÷±ѕя![]() ”лґ‘≥∆÷бѕаљї”Џµг
”лґ‘≥∆÷бѕаљї”Џµг![]() £ђ
£ђ
µ±![]() ±£ђ
±£ђ![]() £ђ
£ђ
°аµг![]() £ђ
£ђ
°а![]() £ђ
£ђ
![]() £ђ
£ђ
![]() Ћƒ±я–ќ
Ћƒ±я–ќ![]() £ђ
£ђ
![]() £ђ
£ђ
…иєэµг![]() ”л
”л![]() ÷б∆љ––µƒ÷±ѕяљїBD”Џµг
÷б∆љ––µƒ÷±ѕяљїBD”Џµг![]() £ђ÷±ѕя
£ђ÷±ѕя![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђ
£ђ
‘т![]() £ђљвµ√
£ђљвµ√![]() £ђ
£ђ
°а÷±ѕя![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђ
£ђ
…и![]() £ђ‘тH£®x£ђ2x-6£©£ђ
£ђ‘тH£®x£ђ2x-6£©£ђ
°а![]() £ђ
£ђ
°а![]() £ђ
£ђ
’ыјнµ√£ђ![]() £ђ
£ђ
љвµ√£Ї![]() £ђ‘т
£ђ‘т![]() £ђ
£ђ
°аµг![]() £ї
£ї
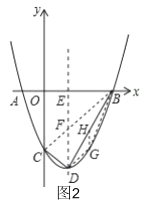
£®3£©іж‘Џ£ђ
”…єіє…ґ®јнµ√£ђ![]() £ђ
£ђ
»зЌЉ3£ђєэµг![]() „ч
„ч![]() љї
љї![]() µƒ—”≥§ѕя”Џ
µƒ—”≥§ѕя”Џ![]() £ђ
£ђ
![]() £ђ
£ђ![]() £ђ
£ђ![]() £ђ
£ђ
![]() £ђ
£ђ![]() ”л
”л![]() ÷бµƒЉ–љ«ґЉ «
÷бµƒЉ–љ«ґЉ «![]() £ђ
£ђ
![]() £ђ
£ђ
”÷![]() £ђ
£ђ
![]() £ђ
£ђ
![]() £ђ
£ђ
![]() “‘
“‘![]() °Ґ
°Ґ![]() °Ґ
°Ґ![]() ќ™ґ•µгµƒ»эљ«–ќ”л
ќ™ґ•µгµƒ»эљ«–ќ”л![]() ѕаЋ∆£ђ
ѕаЋ∆£ђ
![]() “‘
“‘![]() °Ґ
°Ґ![]() °Ґ
°Ґ![]() ќ™ґ•µгµƒ»эљ«–ќ”л
ќ™ґ•µгµƒ»эљ«–ќ”л![]() ѕаЋ∆£ђ
ѕаЋ∆£ђ
![]() їт
їт![]() £ђЉі
£ђЉі![]() їт
їт![]() £ђ
£ђ
љвµ√£Ї![]() їт
їт![]() £ђ
£ђ
єэµг![]() „ч
„ч![]() ÷б”Џ
÷б”Џ![]() £ђ
£ђ
![]() £ђ
£ђ
![]() £ђ
£ђ
Ґўµ±![]() ±£ђ
±£ђ![]() £ђ
£ђ
°а![]() £ђ
£ђ
°аµг![]() £ђ
£ђ
…и÷±ѕя![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђ
£ђ
‘т £ђљвµ√
£ђљвµ√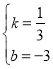 £ђ
£ђ
°а÷±ѕя![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђ
£ђ
Ѕ™ЅҐ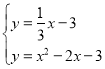 £ђљвµ√£Ї
£ђљвµ√£Ї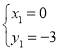 £®…б»•£©£ђ
£®…б»•£©£ђ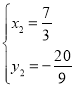 £ђ
£ђ
°аµг![]() £ї
£ї
ҐЏµ±![]() ±£ђ
±£ђ![]() £ђ
£ђ
°а![]() £ђ
£ђ
°аµг![]() £ђ
£ђ
…и÷±ѕя![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђ
£ђ
‘т![]() £ђљвµ√
£ђљвµ√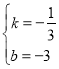 £ђ
£ђ
°а÷±ѕя![]() µƒљвќц љќ™
µƒљвќц љќ™![]() £ђ
£ђ
Ѕ™ЅҐ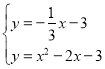 £ђљвµ√
£ђљвµ√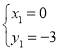 £®…б»•£©£ђ
£®…б»•£©£ђ £ђ
£ђ
![]() µг
µг![]() £ђ
£ђ
„џ…ѕЋщ ц£ђіж‘Џµг![]() їт
їт![]() £ђ є“‘
£ђ є“‘![]() °Ґ
°Ґ![]() °Ґ
°Ґ![]() ќ™ґ•µгµƒ»эљ«–ќ”л
ќ™ґ•µгµƒ»эљ«–ќ”л![]() ѕаЋ∆£Ѓ
ѕаЋ∆£Ѓ



| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њє§»Ћ ¶Єµ”√“їњй≥§ќ™10dm£ђњнќ™6dmµƒЊЎ–ќћъ∆§÷∆„ч“їЄцќёЄ«µƒ≥§Јљће»Ё∆ч£ђ–и“™љЂЋƒљ«Єч≤√µф“їЄц’эЈљ–ќ£Ѓ£®Їсґ»≤їЉ∆£©

£®1£©‘ЏЌЉ÷–ї≠≥ц≤√Љф Њ“вЌЉ£ђ”√ µѕя±н Њ≤√Љфѕя£ђ–йѕя±н Њ’џЇџ£ї≤Ґ«у≥§Јљћеµ„√ж√жїэќ™12dm2 ±£ђ≤√µфµƒ’эЈљ–ќ±я≥§ґаіу£њ
£®2£©»ф“™«у÷∆„чµƒ≥§Јљћеµƒµ„√ж≥§≤їіу”Џµ„√жњнµƒќе±ґ£ђ≤ҐљЂ»Ё∆чљш––Јј–ві¶јн£ђ≤а√ж√њ∆љЈљЈ÷√„µƒЈ—”√ќ™0.5‘™£ђµ„√ж√њ∆љЈљЈ÷√„µƒЈ—”√ќ™2‘™£ђ≤√µфµƒ’эЈљ–ќ±я≥§ґаіу ±£ђ„№Ј—”√„оµЌ£ђ„оµЌќ™ґа…ў£њ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ1£ђ≈„ќпѕяy£љ©Б![]() x2+bx+cµƒґ‘≥∆÷бќ™÷±ѕяx£љ©Б
x2+bx+cµƒґ‘≥∆÷бќ™÷±ѕяx£љ©Б![]() £ђ”лx÷бљї”ЏµгAЇЌµгB£®1£ђ0£©£ђ”лy÷бљї”ЏµгC£ђµгDќ™ѕяґќACµƒ÷–µг£ђ÷±ѕяBD”л≈„ќпѕяљї”ЏЅн“їµгE£ђ”лy÷бљї”ЏµгF£Ѓ
£ђ”лx÷бљї”ЏµгAЇЌµгB£®1£ђ0£©£ђ”лy÷бљї”ЏµгC£ђµгDќ™ѕяґќACµƒ÷–µг£ђ÷±ѕяBD”л≈„ќпѕяљї”ЏЅн“їµгE£ђ”лy÷бљї”ЏµгF£Ѓ
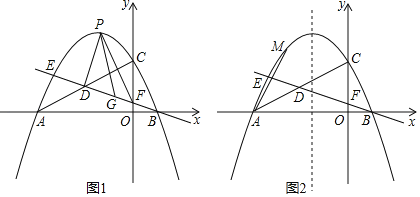
£®1£©«у≈„ќпѕяµƒљвќц љ£ї
£®2£©µгP «÷±ѕяBE…ѕЈљ≈„ќпѕя…ѕ“їґѓµг£ђЅђљ”PD°ҐPF£ђµ±°чPDFµƒ√жїэ„оіу ±£ђ‘ЏѕяґќBE…ѕ’““їµгG£ђ єµ√PG©Б![]() EGµƒ÷µ„о–°£ђ«у≥цPG©Б
EGµƒ÷µ„о–°£ђ«у≥цPG©Б![]() EGµƒ„о–°÷µ£Ѓ
EGµƒ„о–°÷µ£Ѓ
£®3£©»зЌЉ2£ђµгMќ™≈„ќпѕя…ѕ“їµг£ђµгN‘Џ≈„ќпѕяµƒґ‘≥∆÷б…ѕ£ђµгKќ™∆љ√жƒЏ“їµг£ђµ±“‘A°ҐM°ҐN°ҐKќ™ґ•µгµƒЋƒ±я–ќ «’эЈљ–ќ ±£ђ«л«у≥цµгNµƒ„ш±к£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
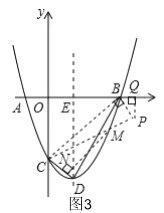
°Њћвƒњ°њ»зЌЉ£ђЋƒ±я–ќABCD÷–£ђCD£љBC£љ4£ђAB£љ1£ђEќ™BC÷–µг£ђ°ѕAED£љ120°г£ђ‘тADµƒ„оіу÷µ «_____£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
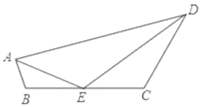
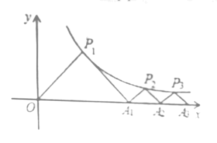
°Њћвƒњ°њ»зЌЉRt°чABC÷–£ђ°ѕACB£љ90°г£ђ°ѕB£љ30°г£ђAC£љ1£ђ«“AC‘Џ÷±ѕяl…ѕ£ђљЂ°чABC»∆µгAЋ≥ ±’л–э„™µљҐў£ђњ…µ√µљµгP1£ђіЋ ±AP1£љ2£їљЂќї÷√Ґўµƒ»эљ«–ќ»∆µгP1Ћ≥ ±’л–э„™µљќї÷√ҐЏ£ђњ…µ√µљµгP2£ђіЋ ±AP2£љ2+![]() £їљЂќї÷√ҐЏµƒ»эљ«–ќ»∆µгP2Ћ≥ ±’л–э„™µљќї÷√Ґџ£ђњ…µ√µљµгP3£ђіЋ ±AP3£љ3+
£їљЂќї÷√ҐЏµƒ»эљ«–ќ»∆µгP2Ћ≥ ±’л–э„™µљќї÷√Ґџ£ђњ…µ√µљµгP3£ђіЋ ±AP3£љ3+![]() £ї°≠∞ііЋєж¬…Љћ–ш–э„™£ђ÷±µљµгP2020ќ™÷є£ђ‘тAP2020µ»”Џ_______£Ѓ
£ї°≠∞ііЋєж¬…Љћ–ш–э„™£ђ÷±µљµгP2020ќ™÷є£ђ‘тAP2020µ»”Џ_______£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њƒ≥√сЋ„¬√”ќіеќ™љ”іэ”ќњЌ„°Ћё–и“™£ђњ™…иЅЋ”–100’≈і≤ќїµƒ¬√єЁ£Ѓµ±√њ’≈і≤ќї√њћм ’Ј—100‘™ ±£ђі≤ќїњ…»Ђ≤њ„в≥ц£Ѓ»ф√њ’≈і≤ќї√њћм ’Ј—ћбЄя20‘™£ђ‘тѕа”¶µЎЉх…ўЅЋ10’≈і≤ќї„в≥ц£Ѓ»зєы√њ’≈і≤ќї√њћм“‘20‘™ќ™µ•ќїћбЄя ’Ј—£ђќ™ є„в≥цµƒі≤ќї…ў«“„вљрЄя£ђƒ«√і√њ’≈і≤ќї√њћм„оЇѕ µƒ ’Ј— «(°°°°)
A. 140‘™ B. 150‘™ C. 160‘™ D. 180‘™
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ»зЌЉ£ђµг![]() £ђµг
£ђµг![]() £ђ°≠µг
£ђ°≠µг![]() ‘ЏЇѓ э
‘ЏЇѓ э![]() µƒЌЉѕу…ѕ£ђ
µƒЌЉѕу…ѕ£ђ ![]() ґЉ «µ»—ь÷±љ«»эљ«–ќ£ђ–±±я
ґЉ «µ»—ь÷±љ«»эљ«–ќ£ђ–±±я![]() ґЉ‘Џ
ґЉ‘Џ![]() ÷б…ѕ(
÷б…ѕ(![]() «іу”Џїтµ»”Џ2µƒ’э э э)£ђ‘т
«іу”Џїтµ»”Џ2µƒ’э э э)£ђ‘т![]() __________£Ѓ£®”√Їђ
__________£Ѓ£®”√Їђ![]() µƒ љ„”±н Њ£©
µƒ љ„”±н Њ£©
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ“—÷™≈„ќпѕя![]() µƒґ•µг
µƒґ•µг![]() ‘Џ
‘Џ![]() ÷б…ѕ£Ѓ
÷б…ѕ£Ѓ
£®1£©»фµг![]() «≈„ќпѕя„оµЌµг£ђ«“¬д‘Џ
«≈„ќпѕя„оµЌµг£ђ«“¬д‘Џ![]() ÷б’э∞л÷б…ѕ£ђ÷±љ”–і≥ц
÷б’э∞л÷б…ѕ£ђ÷±љ”–і≥ц![]() µƒ»°÷µЈґќІ£ї
µƒ»°÷µЈґќІ£ї
£®2£©![]() £ђ
£ђ![]() «≈„ќпѕя…ѕЅљµг£ђ»ф
«≈„ќпѕя…ѕЅљµг£ђ»ф![]() £ђ‘т
£ђ‘т![]() £ї»ф
£ї»ф![]() £ђ‘т
£ђ‘т![]() £ђ«“µ±
£ђ«“µ±![]() µƒЊшґ‘÷µќ™4 ±£ђ
µƒЊшґ‘÷µќ™4 ±£ђ![]() ќ™µ»—ь÷±љ«»эљ«–ќ£®∆д÷–
ќ™µ»—ь÷±љ«»эљ«–ќ£®∆д÷–![]() £©£Ѓ
£©£Ѓ
Ґў«у≈„ќпѕяµƒљвќц љ£ї
ҐЏ…и![]() ÷–µгќ™
÷–µгќ™![]() £ђ»ф
£ђ»ф![]() £ђ«уµг
£ђ«уµг![]() „Ё„ш±кµƒ„о–°÷µ£Ѓ
„Ё„ш±кµƒ„о–°÷µ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї
°Њћвƒњ°њ£®1£©÷±ѕяl1£Їy£љx+1”лx÷бљї”ЏµгA£ђ÷±ѕяl2£Їy£љ©Бx+3”лx÷бљї”ЏµгB£ђl1”лl2љї”ЏµгC£ђ÷±ѕяl3єэѕяґќABµƒ÷–µгЇЌµгC£ђ«у÷±ѕяl3µƒљвќц љ£ї
£®2£©“—÷™∆љ√ж÷±љ«„ш±кѕµ÷–£ђ÷±ѕяlЊ≠єэµгP£®2£ђ1£©«“”лЋЂ«ъѕяy£љ![]() љї”ЏA°ҐB≤їЌђЅљµг£ђќ «Јсіж‘Џ’в—щµƒ÷±ѕяl£ђ єµ√µгP«°Ї√ќ™ѕяґќABµƒ÷–µг£ђ»фіж‘Џ£ђ«у≥ц÷±ѕяlµƒљвќц љ£ђ»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£ї
љї”ЏA°ҐB≤їЌђЅљµг£ђќ «Јсіж‘Џ’в—щµƒ÷±ѕяl£ђ єµ√µгP«°Ї√ќ™ѕяґќABµƒ÷–µг£ђ»фіж‘Џ£ђ«у≥ц÷±ѕяlµƒљвќц љ£ђ»ф≤їіж‘Џ£ђ«лЋµ√чјн”…£ї
£®3£©»фA£®x1£ђy1£©°ҐB£®x2£ђy2£© «≈„ќпѕяy£љ4x2…ѕµƒ≤їЌђЅљµг£®y1°ўy2£©£ђѕяґќABµƒіє÷±∆љЈ÷ѕя”лy÷бљї”ЏµгP£ђ”лѕяґќABљї”ЏµгM£®xm£ђym£©£ђ‘т≥∆ѕяґќABќ™µгPµƒ“їћх°∞ѕаєЎѕ“°±£ђ»фµгPµƒ„ш±кќ™£®0£ђa£© ±£®aќ™≥£ э£©£ђ÷§√чµгPµƒ°∞ѕаєЎѕ“°±÷–µгMµƒ„Ё„ш±кѕаЌђ£Ѓ
≤йњіір∞ЄЇЌљвќц>>
∞ўґ»÷¬–≈ - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com