
 与双曲线
与双曲线 相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
相交于A(-1,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是1.
 x+
x+
 与双曲线
与双曲线 相交于A(-1,a)、B两点可得B点横坐标为1,点C的坐标为(1,0),再根据△AOC的面积为1可求得点A的坐标,从而求得结果;
相交于A(-1,a)、B两点可得B点横坐标为1,点C的坐标为(1,0),再根据△AOC的面积为1可求得点A的坐标,从而求得结果; 与双曲线
与双曲线 相交于A(-1,a)、B两点,
相交于A(-1,a)、B两点, ,
, 可得m=-1,n=-1;
可得m=-1,n=-1;  解得k=-
解得k=- ,b=
,b= .
. x+
x+ .
.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源:不详 题型:解答题
 的图象和反比例函数
的图象和反比例函数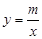 的图象的两个交点.
的图象的两个交点.
 与
与 轴的交点
轴的交点 的坐标及△
的坐标及△ 的面积;
的面积; 的解集(请直接写出答案).
的解集(请直接写出答案).查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.
与一次函数y=mx+b的图象交于P(-2,1)和Q(1,n)两点.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 与x轴、y轴分别交于A、B两点,C为OA中点;
与x轴、y轴分别交于A、B两点,C为OA中点;
 个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;
个单位长度的速度向终点B运动,过点Q作QM∥AB交x轴于点M,若线段PM的长为y,点P运动时间为t( ),求y于t的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与x轴、y轴的交点分别为A、B,以B为旋转中心,将△BOA逆时针旋转,得△BCD(其中O与C、A与D是对应的顶点).
的图象与x轴、y轴的交点分别为A、B,以B为旋转中心,将△BOA逆时针旋转,得△BCD(其中O与C、A与D是对应的顶点).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 只同一型号的零件,他们生产的零件
只同一型号的零件,他们生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
(分)的函数关系的图象如图所示。根据图象提供的信息解答下列问题:
 倍,请分别求出甲、乙两人生产全过程中,生产的零件
倍,请分别求出甲、乙两人生产全过程中,生产的零件 (只)与生产时间
(只)与生产时间 (分)的函数关系式;
(分)的函数关系式;查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图像经过点A、C.
的图像经过点A、C.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达
两港同时出发,相向而行,两船在静水中速度相同,水流速度为5千米/小时,甲船逆流而行4小时到达 港.下图表示甲观光船距
港.下图表示甲观光船距 港的距离
港的距离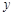 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,结合图象解答下列问题:
(小时)之间的函数关系式,结合图象解答下列问题:
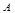 、
、 两港距离 千米,船在静水中的速度为 千米/小时;
两港距离 千米,船在静水中的速度为 千米/小时; 港的距离
港的距离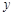 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象;
(小时)之间的函数图象;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com