
 如图,AD∥EF∥BC,EG分别交AB、DB、AC于点E、F、G,若AD=9,BC=12,且AE:EB=2:1,则FG=5.
如图,AD∥EF∥BC,EG分别交AB、DB、AC于点E、F、G,若AD=9,BC=12,且AE:EB=2:1,则FG=5. 分析 根据AD∥EF∥BC即可得出$\frac{EG}{BC}$=$\frac{AE}{AB}=\frac{AE}{AE+EB}$、$\frac{EF}{AD}=\frac{BE}{AB}=\frac{BE}{AE+EB}$,再结合AD=9,BC=12,且AE:EB=2:1,即可得出EG、EF的长,根据FG=EG-EF即可得出结论.
解答 解:∵EF∥BC,BC=12,AE:EB=2:1,
∴$\frac{EG}{BC}$=$\frac{AE}{AB}=\frac{AE}{AE+EB}$=$\frac{2}{3}$,
∴EG=$\frac{2}{3}$BC=8.
∵AD∥EF,AD=9,AE:EB=2:1,
∴$\frac{EF}{AD}=\frac{BE}{AB}=\frac{BE}{AE+EB}$=$\frac{1}{3}$,
∴EF=$\frac{1}{3}$AD=3.
∴FG=EG-EF=8-3=5.
故答案为:5.
点评 本题考查了平行线的性质,解题的关键是求出EG、EF的长.本题属于基础题,难度不大,解决该题型题目时,根据平行线的性质得出线段之间的比例关系是关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB.
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
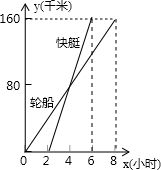 如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中随时间变化的图象(分别是正比例函数和一次函数图象),根据图象解答下列问题;
如图,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中随时间变化的图象(分别是正比例函数和一次函数图象),根据图象解答下列问题;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com