
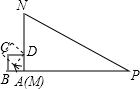
 如图,在Rt△MNP中,∠N=60°,MN=3,NP=6,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD沿边MN→NP进行翻滚,直到正方形有一个顶点与P重合即停止滚动,正方形在整个翻滚过程中,点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是( )
如图,在Rt△MNP中,∠N=60°,MN=3,NP=6,正方形ABCD的边长为1,它的一边AD在MN上,且顶点A与M重合.现将正方形ABCD沿边MN→NP进行翻滚,直到正方形有一个顶点与P重合即停止滚动,正方形在整个翻滚过程中,点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积是( )| A. | $\frac{7π}{3}$+2 | B. | 2π+2 | C. | $\frac{7π}{3}$ | D. | $\frac{4π}{3}$ |
分析 第一次翻滚:绕D,点A围成的扇形是圆心角是90°,半径是1;
第二次翻滚:绕C,点A围成的图形是扇形和两个三角形,扇形是圆心角是90°,半径是$\sqrt{2}$,两个等腰直角三角形组成一个边长为1的正方形;
第三次翻滚:绕B,点A围成的扇形是圆心角是210°,半径是1;
第四次翻滚:绕A,点A不动;
第五次翻滚:绕D,点A围成的扇形是圆心角是90°,半径是1;
…
依次重复,直到第八次翻滚结束.
解答 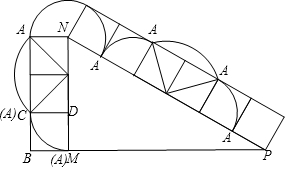 解:如图,
解:如图,
点A所经过的路线与Rt△MNP的两边MN、NP所围成的图形的面积:
S=$\frac{90π×{1}^{2}}{360}$×3+$\frac{90π×(\sqrt{2})^{2}}{360}$×2+$\frac{210π×{1}^{2}}{360}$+2
=$\frac{π}{4}$×3+$\frac{π}{2}$×2+$\frac{7π}{12}$+2
=$\frac{7π}{3}$+2.
点评 本题考查了点的轨迹的问题,考查了正方形的性质和翻滚的性质,正方形的边长相等,且每一个角都是90°,熟练掌握扇形面积公式:S=$\frac{nπ{R}^{2}}{360}$(n是圆心角的度数,R是扇形的半径);此类点的轨迹题比较难,关键是正确画出图形,有空间想象能力,动手操作,得出结论.


科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{1}{2}$x | B. | y=2x | C. | y=$\frac{2}{x}$ | D. | y=-$\frac{1}{2}$x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=$\frac{1}{b}$ | B. | a=-$\frac{1}{b}$ | C. | a=b | D. | a=-b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若ab=1,则a与b互为倒数 | B. | 若ab<0,则$\frac{a}{b}$<0 | ||
| C. | 若a+b=0,则$\frac{a}{b}$=-1 | D. | 若$\frac{a}{b}$>0,则ab>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com