
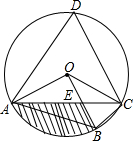
 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连结OA、OB、OC、AC,OB与AC相交于点E.
如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连结OA、OB、OC、AC,OB与AC相交于点E.分析 (1)根据四边形ABCD是⊙O的内接四边形得到∠ABC+∠D=180°,根据∠ABC=2∠D得到∠D+2∠D=180°,从而求得∠D=60°,进而得出答案;
(2)首先根据∠AOB=3∠COB得到∠COB=30°,从而得到∠AOB为直角,然后利用S阴影=S扇形OBA-S△OEA求解.
解答 解:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠ABC+∠D=180°,
∵∠ABC=2∠D,
∴∠D+2∠D=180°,
∴∠D=60°,
∴∠AOC=2∠D=120°;
(2)∵∠AOB=3∠COB,
∴∠AOC=∠AOB+3∠COB=120°,
∴∠COB=30°,
∴∠AOB=∠BOC-∠AOB=90°,
在Rt△OCE中,OC=4$\sqrt{3}$,
∴OE=OA•tan∠OAE=4$\sqrt{3}$•tan30°=4$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=4,
∴S△OEA=$\frac{1}{2}$OE•OA=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$,
∴S扇形OBA=$\frac{90π(4\sqrt{3})^{2}}{360}$=12π,
∴S阴影=S扇形OBA-S△OEA=12π-4$\sqrt{3}$.
点评 本题考查了扇形面积的计算,圆内接四边形的性质,解直角三角形的知识,在求不规则的阴影部分的面积时常常转化为几个规则几何图形的面积的和或差.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是城市中某区域的示意图,小聪同学从点O出发,先向西走100米,再向南走200米到达学校,如果学校的位置用(-100,-200)表示,那么(300,200)表示的地点是超市.
如图是城市中某区域的示意图,小聪同学从点O出发,先向西走100米,再向南走200米到达学校,如果学校的位置用(-100,-200)表示,那么(300,200)表示的地点是超市.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB且∠AOC,∠AOB在OA的异侧,则OC的方向是北偏东70°.
如图,OA的方向是北偏东15°,OB的方向是北偏西40°,若∠AOC=∠AOB且∠AOC,∠AOB在OA的异侧,则OC的方向是北偏东70°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 分数/分 | 7 | 8 | 9 | 10 |
| 频数 | 2 | 9-x | x+14 | 24 |
| A. | 众数、方差 | B. | 中位数、方差 | C. | 众数、中位数 | D. | 平均数、中位数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com