
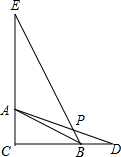
 已知,Rt△ABC中∠C=90°,点D在边CB的延长线上,BD=AC,点E在边CA的延长线上,AE=CD,连接BE、AD交于点P,若BC=2BD=2,则PE=$\frac{{9\sqrt{5}}}{5}$.
已知,Rt△ABC中∠C=90°,点D在边CB的延长线上,BD=AC,点E在边CA的延长线上,AE=CD,连接BE、AD交于点P,若BC=2BD=2,则PE=$\frac{{9\sqrt{5}}}{5}$. 分析 过B作BH∥EC,可得△BHD∽△CAD,根据相似三角形的性质可设BP=m,则PE=9m,由勾股定理可求m,进一步求得PE的长.
解答 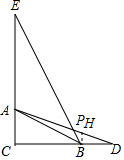 解:由已知得,BC=2,BD=1,
解:由已知得,BC=2,BD=1,
∵BD=AC,AE=CD,
∴AE=3,AC=1,
过B作BH∥EC,
∵BH∥EC,
∴△BHD∽△CAD,
∴$\frac{BH}{AC}$=$\frac{BD}{CD}$,
∴$\frac{BH}{1}$=$\frac{1}{3}$,
∴BH=$\frac{1}{3}$,
∵BH∥AE,
∴△HBP∽△AEP,
∴$\frac{BP}{PE}$=$\frac{\frac{1}{3}}{3}$=$\frac{1}{9}$,
设BP=m,则PE=9m,
∴BE=10m,
在Rt△ECB中,由勾股定理得(10m)2=22+42,
100m2=20,
m2=$\frac{1}{5}$,
m=$\frac{\sqrt{5}}{5}$,
PE=$\frac{{9\sqrt{5}}}{5}$.
故答案为:$\frac{{9\sqrt{5}}}{5}$.
点评 本题考查了相似三角形的判定与性质以及勾股定理,作出辅助线构造三角形相似是解决问题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
套餐类型 | 月费(元/月) | 套餐内包含内容 | 套餐外资费 | ||
| 国内数据流量 | 国内电话(分钟) | 流量 | 国内 电话 | ||
| 套餐1 | 76 | 400M | 200 | 0M-200M时,0.3元/M 201M-1G时,60元 | 0.15元/分钟 |
| 套餐2 | 106 | 800M | 300 | ||
| 套餐3 | 136 | 1G | 500 | ||
| 套餐4 | 166 | 2G | 500 | ||
| A. | 套餐1 | B. | 套餐2 | C. | 套餐3 | D. | 套餐4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x/kg | 0 | 1 | 2 | 3 | … |
| y/cm | 4 | 4.2 | 4.4 | 4.6 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com