
分析 (1)设今年5月份A款汽车每辆售价为x万元,则去年同期A款汽车每辆售价为(x+1)万元,根据数量=总价÷单价结合今年5月份与去年同期销售数量相等,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)设B款汽车卖出m辆,则A款汽车卖出(15-m)辆,根据总利润=单辆利润×销售数量结合获利不低于38万元,即可得出关于m的一元一次不等式,解之取其最小值即可.
解答 解:(1)设今年5月份A款汽车每辆售价为x万元,则去年同期A款汽车每辆售价为(x+1)万元,
根据题意得:$\frac{90}{x+1}$=$\frac{80}{x}$,
解得:x=8,
经检验,x=8是原方程的解.
答:今年5月份A款汽车每辆售价为8万元.
(2)设B款汽车卖出m辆,则A款汽车卖出(15-m)辆,
根据题意得:(10.5-7.5)×m+(8-6)×(15-m)≥38,
解得:m≥8.
答:若卖出这两款汽车15辆后获利不低于38万元,B款汽车至少卖出8辆.
点评 本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)数量=总价÷单价结合今年5月份与去年同期销售数量相等,列出关于x的分式方程;(2)根据总利润=单辆利润×销售数量结合获利不低于38万元,列出关于m的一元一次不等式.


科目:初中数学 来源: 题型:解答题
 某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.| 进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
| 人数 | 2 | 1 | 4 | 7 | 8 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 运动会上,甲、乙、丙三位同学进行跳绳比赛,通过“手心手背”游戏决定谁先跳,规则如下:三个人同时各用一只手随机出示手心或手背,若其中有一个人的手势与另外两个不同,则此人先进行比赛,若三个人手势相同,则重新决定,那么通过一次“手心手背”游戏,甲同学先跳绳的概率是多少?
运动会上,甲、乙、丙三位同学进行跳绳比赛,通过“手心手背”游戏决定谁先跳,规则如下:三个人同时各用一只手随机出示手心或手背,若其中有一个人的手势与另外两个不同,则此人先进行比赛,若三个人手势相同,则重新决定,那么通过一次“手心手背”游戏,甲同学先跳绳的概率是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
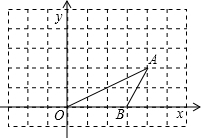 如图,点O、A、B的坐标分别为(0,0),(4,2),(3,0),将△OAB绕点O按逆时针方向旋转90°得到△OA′B′.
如图,点O、A、B的坐标分别为(0,0),(4,2),(3,0),将△OAB绕点O按逆时针方向旋转90°得到△OA′B′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com