
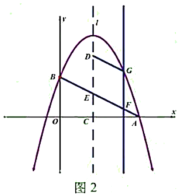
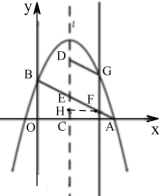
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的一个交点为点
轴的一个交点为点![]() ,与
,与![]() 轴的交点为点
轴的交点为点![]() ,抛物线的对称轴
,抛物线的对称轴![]() 与
与![]() 轴交于点
轴交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() ,点
,点![]() 是对称轴
是对称轴![]() 上一动点.
上一动点.

(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)如图2,抛物线的对称轴![]() 向右平移与线段
向右平移与线段![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,当四边形
,当四边形![]() 是平行四边形且周长最大时,求出点
是平行四边形且周长最大时,求出点![]() 的横坐标.
的横坐标.
【答案】(1)![]() ,
,![]() ;(2)存在,
;(2)存在,![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
(1)令x=0,求出y值可得B点坐标,令y=0,求出x值,根据点A在对称轴右侧可得点A坐标;
(2)根据抛物线解析式可求出对称轴为直线x=![]() ,根据A、B坐标可得直线AB的解析式,进而可求出点E坐标,即可求出CE的长,分
,根据A、B坐标可得直线AB的解析式,进而可求出点E坐标,即可求出CE的长,分![]() 、
、![]() 、
、![]() 三种情况,分别利用相似三角形的性质求出点D坐标即可得答案;
三种情况,分别利用相似三角形的性质求出点D坐标即可得答案;
(3)过点![]() 做
做![]() ,设
,设![]() ,
,![]() ,可用m表示出FG的长,利用勾股定理可求出AB的长,根据平移的性质可用m表示出FH的长,由平行线的性质可得
,可用m表示出FG的长,利用勾股定理可求出AB的长,根据平移的性质可用m表示出FH的长,由平行线的性质可得![]() ,即可证明△BOA∽△EHF,根据相似三角形的性质可用m表示出EF的长,即可用m表示出平行四边形
,即可证明△BOA∽△EHF,根据相似三角形的性质可用m表示出EF的长,即可用m表示出平行四边形![]() 的周长,根据二次函数的性质即可得答案.
的周长,根据二次函数的性质即可得答案.
(1)令x=0得:y=3,
∴点B坐标为(0,3),
令y=0得:![]() =0,
=0,
解得:x1=-1,x2=6,
∵点A在对称轴右侧,
∴点A坐标为(6,0),
故答案为:![]() ,
,![]()
(2)存在,理由如下:
∵抛物线解析式为![]() ,
,
∴对称轴为直线 ,
,
设直线AB的解析式为y=kx+b,
∵A(6,0),B(0,3)
∴![]() ;
;
解得: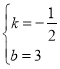 ,
,
∴直线![]() 的解析式为
的解析式为![]()
∴当![]() 时,
时,![]() ,即E(
,即E(![]() ,
,![]() ),
),
∴![]()
①如图,当![]() 时,
时,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
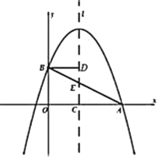
②当![]() 时,过点B作BF⊥l于F,
时,过点B作BF⊥l于F,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵对称轴为直线![]() ,
,
∴![]() ,EF=CF-CE=
,EF=CF-CE=![]() ,
,
∵∠BDF+∠DBF=90°,∠EBF+∠DBF=90°,
∴∠BDF=∠EBF,
∵∠BFD=∠BFE,
∴![]() ,
,
∴![]() ,即
,即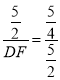 ,
,
解得:DF=5,
∴CD=CF+DF=3+5=8,
∴![]() .
.

③当![]() 时,不合题意舍去.
时,不合题意舍去.
综上所述:![]() 或
或![]() .
.
(3)过点![]() 做
做![]() ,设
,设![]() ,
,![]() ,
,
∴![]() ,
,
∵抛物线的对称轴![]() 向右平移与线段
向右平移与线段![]() 交于点
交于点![]() ,
,
∴![]() ,
,
∵OA=6,OB=3,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴△BOA∽△EHF,
∴![]() ,即
,即 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 时平行四边形周长最大,
时平行四边形周长最大,
∴![]() 的横坐标为
的横坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点E在矩形ABCD对角线AC上由A向C运动,且BC=2![]() ,∠ACB=30°,连结EF,过点E作EF⊥DE,交BC于点F(当点F与点C重合时,点E也停止运动)
,∠ACB=30°,连结EF,过点E作EF⊥DE,交BC于点F(当点F与点C重合时,点E也停止运动)
(1)如图1,当AC平分角∠DEF时,求AE的长度;
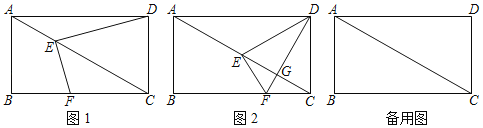
(2)如图2,连结DF,与AC交于点G,若DF⊥AC时,求四边形DEFC的面积;
(3)若点E分AC为1:2两部分时,求BF:FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() (
(![]() 左
左![]() 右)两点,交
右)两点,交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() .
.
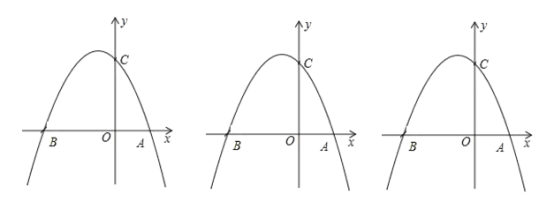
(1)求抛物线的解析式;
(2)点![]() 为第二象限抛物线上一点,连接
为第二象限抛物线上一点,连接![]() 、
、![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 做
做![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,过点
,过点![]() 做直线
做直线![]() 轴,在
轴,在![]() 轴上方直线
轴上方直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,当
,当![]() 时,求线段
时,求线段![]() 的长;
的长;
(3)在(2)的条件下,点![]() 为第二象限抛物线上的一点,连接
为第二象限抛物线上的一点,连接![]() ,过点
,过点![]() 做
做![]() 于点
于点![]() ,连接
,连接![]() ,线段
,线段![]() 、
、![]() 分别交线段
分别交线段![]() 于点
于点![]() 、
、![]() ,当
,当![]() 时,求
时,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的
的![]() 与
与![]() 的部分对应值如表:
的部分对应值如表:
|
|
|
|
|
|
|
|
|
|
|
|
下列结论:![]() 抛物线的开口向上;②抛物线的对称轴为直线
抛物线的开口向上;②抛物线的对称轴为直线![]() ;③当
;③当![]() 时,
时,![]() ;④抛物线与
;④抛物线与![]() 轴的两个交点间的距离是
轴的两个交点间的距离是![]() ;⑤若
;⑤若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中正确的个数是( )
,其中正确的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
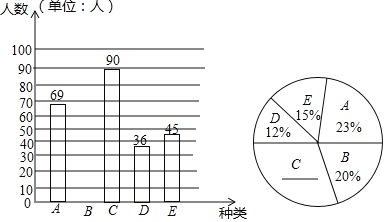
【题目】某中学为了了解在校学生对校本课程的喜爱情况,随机调查了九年级学生对A,B,C,D,E五类校本课程的喜爱情况,要求每位学生只能选择一类最喜欢的校本课程,根据调查结果绘制了如下的两个统计图.
请根据图中所提供的信息,完成下列问题:
(1)本次被调查的学生的人数为 ;
(2)补全条形统计图;
(3)扇形统计图中,C类所在扇形的圆心角的度数为 ;
(4)若该中学有4000名学生,请估计该校喜爱C,D两类校本课程的学生共有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导“绿色出行,低碳生活”的号召,今年春天,安庆市的街头出现了一道道绿色的风景线--“共享单车”. 图(1)所示的是一辆共享单车的实物图. 图(2)是这辆共享单车的部分几何示意图,其中车架档AC长为40cm,座杆CE的长为18cm. 点A、C、E在同一条直线上,且∠CAB=60°,∠ACB=75°
(1)求车座点E到车架档AB的距离;
(2)求车架档AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com