
分析 (1)根据一元一次不等式组的解法,首先求出每个不等式的解集,再求出这些解集的公共部分即可.
(2)根据分式的混合运算顺序,首先计算小括号里面的,然后计算除法,求出算式$\frac{3-a}{2a-4}$÷(a+2-$\frac{5}{a-2}$)的值是多少即可.
解答 解:(1)由x-1>2x,可得x<-1,
由$\frac{1}{2}x+3<-1$,可得x<-8,
∴不等式$\left\{\begin{array}{l}{x-1>2x}\\{\frac{1}{2}x+3<-1}\end{array}\right.$的解集是:
x<-8.
(2)$\frac{3-a}{2a-4}$÷(a+2-$\frac{5}{a-2}$)
=$\frac{3-a}{2a-4}$÷$\frac{{a}^{2}-9}{a-2}$
=-$\frac{1}{2a+6}$
点评 (1)此题主要考查了一元一次不等式组的解法,要熟练掌握,解答此题的关键是要明确:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.
(2)此题还考查了分式的混合运算,要注意运算顺序,分式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.


科目:初中数学 来源: 题型:选择题
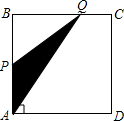 如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )
如图,四边形ABCD是矩形,AB=8,BC=4,动点P以每秒2个单位的速度从点A沿线段AB向B点运动,同时动点Q以每秒3个单位的速度从点B出发沿B-C-D的方向运动,当点Q到达点D时P、Q同时停止运动,若记△PQA的面积为y,运动时间为x,则下列图象中能大致表示y与x之间函数关系图象的是( )| A. | 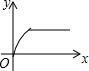 | B. | 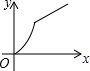 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:| A. | ①② | B. | 只有① | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
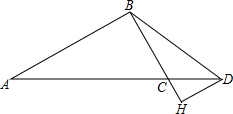 如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.
如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.
如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
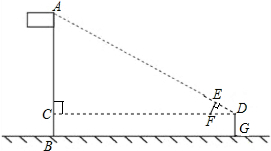 如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.
如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com