
分析 (1)原式第一项利用乘方的意义计算,第二项利用零指数幂法则计算,第三项利用负整数指数幂法则计算即可得到结果;
(2)原式利用幂的乘方与积的乘方运算法则计算,再利用同底数幂的乘法法则计算,合并即可得到结果;
(3)原式结合后,利用平方差公式及完全平方公式计算即可得到结果;
(4)原式利用平方差公式化简,再利用完全平方公式计算即可得到结果.
解答 解:(1)原式=-8+$\frac{1}{3}$-9=-16$\frac{2}{3}$;
(2)原式=tm+2+tm+2=2tm+2;
(3)原式=(x2-9)(x2-9)=x4-18x2+81;
(4)原式=(2a-3)2-b2=4a2-12a-b2+9.
点评 此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
 小明从家骑自行车出发,沿一条直路到相距2400米的移动公司办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局同一条道路步行回家,小明在邮局停留2分钟后沿原路原原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD,线段EF分别表示S1、S2与t之间的函数关系的图象.
小明从家骑自行车出发,沿一条直路到相距2400米的移动公司办事,小明出发的同时,他的爸爸以96米/分钟的速度从邮局同一条道路步行回家,小明在邮局停留2分钟后沿原路原原速返回,设他们出发后经过t分钟时,小明与家之间的距离为S1米,小明爸爸与家之间的距离为S2米,图中折线OABD,线段EF分别表示S1、S2与t之间的函数关系的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成本(元/个) | 售价 (元/个) | |
| A | 2 | 2.4 |
| B | 3 | 3.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1,2,3 | B. | 32,42,52 | C. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
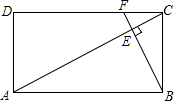 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}$=$\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{1}{16}$.
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}$=$\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于$\frac{1}{16}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com