
【题目】阅读下列材料,并用相关的思想方法解决问题.
例:若多项式![]() 分解因式的结果中有因式
分解因式的结果中有因式![]() ,求实数
,求实数![]() 的值.
的值.
解:设![]()
若![]() ,则
,则![]() 或
或![]()
由![]() 得
得![]()
则![]() 是方程
是方程![]() 的解
的解
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
解决问题:(1)若多项式![]() 分解因式的结果中有因式
分解因式的结果中有因式![]() ,求实数
,求实数![]() 的值;
的值;
(2)若多项式![]() 分解因式的结果中有因式
分解因式的结果中有因式![]() 和
和![]() .
.
①求出![]() 、
、![]() 的值;
的值;
②直接写出方程![]() 的解.
的解.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个大小、质地都相同的乒乓球,球面上分别标有数字1、2、3、4.
(1)搅匀后从中任意摸出1个球,求摸出的乒乓球球面上数字为1的概率;
(2)搅匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,求2次摸出的乒乓球球面上数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
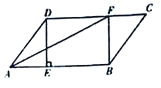
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知C是线段AB上的一点,分别以AC、BC为边在线段AB同侧作正方形ACDE和正方形CBGF,点F在CD上,联结AF、BD,BD与FG交于点M,点N是边AC上的一点,联结EN交AF 与点H.
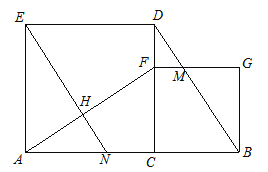
(1)求证:AF=BD;
(2)如果![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设某商场地下停车场有5个出入口,每天早晨7点开始对外停车且此时车位空置率为90%,在每个出入口的车辆数均是匀速出入的情况下,如果开放2个进口和3个出口,6小时车库恰好停满;如果开放3个进口和2个出口,3小时车库恰好停满.2019年清明节期间,由于商场人数增多,早晨7点时的车位空置率变为60%,因为车库改造,只能开放1个进口和1个出口,则从早晨7点开始经过______小时车库恰好停满.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
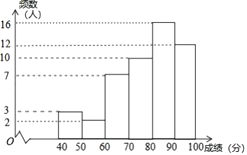
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E是BC边的中点,动点M在CD边上运动,以EM为折痕将△CEM折叠得到△PEM,连接PA,若AB=4,∠BAD=60°,则PA的最小值是_____.
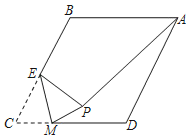
查看答案和解析>>
科目:初中数学 来源: 题型:
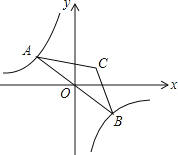
【题目】如图,已知反比例函数y=﹣![]() 的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为__.
的图象与直线y=kx(k<0)相交于点A、B,以AB为底作等腰三角形,使∠ACB=120°,且点C的位置随着k的不同取值而发生变化,但点C始终在某一函数图象上,则这个图象所对应的函数解析式为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com