
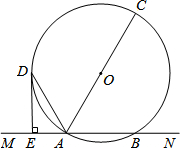 如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线.
如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,求证:DE是⊙O的切线.  优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:解答题
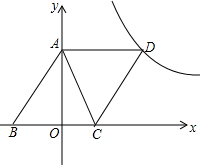 如图,已知,A(0,4),B(-3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=$\frac{k}{x}$的图象经过D点.
如图,已知,A(0,4),B(-3,0),C(2,0),D为B点关于AC的对称点,反比例函数y=$\frac{k}{x}$的图象经过D点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
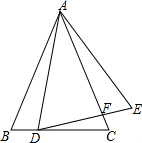 如图,在△ABC中,AB=AC,点D在边BC上,连接AD,将线段AD绕点A逆时针旋转到AE,使得∠DAE=∠BAC,连接DE交AC于F,请写出图中一对相似的三角形:△ABD∽AEF(只要写出一对即可).
如图,在△ABC中,AB=AC,点D在边BC上,连接AD,将线段AD绕点A逆时针旋转到AE,使得∠DAE=∠BAC,连接DE交AC于F,请写出图中一对相似的三角形:△ABD∽AEF(只要写出一对即可).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
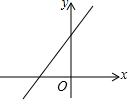 已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,则y1与y2的大小关系是( )
已知点A(-2,y1)和点B(1,y2)是如图所示的一次函数y=2x+b图象上的两点,则y1与y2的大小关系是( )| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | y1≥y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米)
图1是某游乐场的摩天轮,图2是它的正面示意图,已知摩天轮的半径为40米,每分钟绕圆心O匀速旋转15°,其最低点A离地面的距离AB为5米,小明从点A处登上摩天轮,5分钟后旋转到点C,此时小明绕点O旋转了多少度?他离地面的高度CD是多少米?(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com