
【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);

(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
【答案】(1)画图见解析;(2)(2)弧AD的长为![]() π.
π.
【解析】分析: (1)作∠ABC的平分线,与AC的交点就是圆心P,此时⊙P与AB,BC两边都相切;如图,作BC的垂线PD,证明PD和半径相等即可,根据角平分线的性质可得:PA=PD.
(2)要想求劣弧AD的长,根据弧长公式需求圆心角∠APD的半径AP的长,利用四边形的内角和求∠APD=135°,再利用勾股定理和等腰三角形的性质求出AP=PD=DC=![]() 1,代入公式可求弧长.
1,代入公式可求弧长.
详解:
(1)作∠ABC的角平分线交AC于点P,以点P为圆心,AP为半径作圆.

(2)如图,∵P与AB,BC两边都相切,
∴∠BAP=∠BDP=90°,
∵∠ABC=45°,
∴∠APD=360°90°90°45°=135°,
∴∠DPC=45°,
∴△DPC是等腰直角三角形,
∴DP=DC,
在Rt△ABC中,AB=AC=1,
∴CB=![]() ,
,
∵BP=BP,AP=PD,
∴Rt△ABP≌Rt△DBP,
∴BD=AB=1,
∴CD=PD=AP=![]() 1,
1,
∴劣弧AD的长=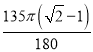 =
=![]() .
.
点睛: 本题考查了切线的判定、圆的作图以及弧长的计算,首先掌握切线的判定方法:①无交点,作垂线段,证半径;②有交点,作半径,证垂直;本题利用了第①种判定方法;并熟练掌握弧长计算公式:l=![]() (弧长为l,圆心角度数为n,圆的半径为R).
(弧长为l,圆心角度数为n,圆的半径为R).


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
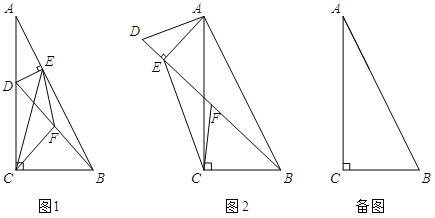
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数 y=kx+b 的图像如图所示,则当kx+b>0 时,x 的取值范围为___________.

【答案】x>1
【解析】分析:题目要求 kx+b>0,即一次函数的图像在x 轴上方时,观察图象即可得x的取值范围.
详解:
∵kx+b>0,
∴一次函数的图像在x 轴上方时,
∴x的取值范围为:x>1.
故答案为:x>1.
点睛:本题考查了一次函数与一元一次不等式的关系,主要考查学生的观察视图能力.
【题型】填空题
【结束】
16
【题目】菱形ABCD中, ![]() ,其周长为32,则菱形面积为____________.
,其周长为32,则菱形面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
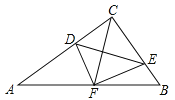
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别在AC,BC上,且∠CDE=∠B,将△CDE沿DE折叠,点C恰好落在AB边上的点F处.若AC=8,AB=10,则CD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
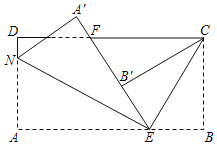
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.
(1)若∠BEB′=110°,则∠BEC= °,∠AEN= °,∠BEC+∠AEN= °.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠AEN的度数.(提示,长方形的四个角都是90°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方法感悟:
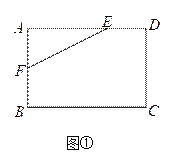
(1)如图①,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决:
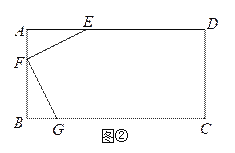
(2)如图②,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面上有四个点A、B、C、D,请用直尺按下列要求作图:
(1)作直线AB;
(2)作射线BC;
(3)连接AD,并将其反向延长至E,使DE=2AD;
(4)找到一点F,使点F到A、B、C、D四点的距离之和最短.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是![]() =610千克,
=610千克, ![]() =609千克,亩产量的方差分别是
=609千克,亩产量的方差分别是![]() =29.6,
=29.6, ![]() =2.则关于两种小麦推广种植的合理决策是( )
=2.则关于两种小麦推广种植的合理决策是( )
A. 甲的平均亩产量较高,应推广甲
B. 甲、乙的平均亩产量相差不多,均可推广
C. 甲的平均亩产量较高,且亩产量比较稳定,应推广甲
D. 甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com