
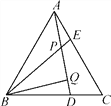
【题目】如图,等边△ABC中,AE=CD,AD,BE相交于点P,BQ⊥AD于点Q.
(1)求证:BP=2PQ;
(2)若PE=1,PQ=3,试求AD的长.
【答案】(1)见解析;(2)7
【解析】试题分析:![]() 根据全等三角形的判定方法SAS可证得△BEC≌△ADB,根据各角的关系及三角形内角、外角和定理可证得
根据全等三角形的判定方法SAS可证得△BEC≌△ADB,根据各角的关系及三角形内角、外角和定理可证得![]() ,即可得结论.
,即可得结论.
![]() 由已知条件,先证明△ABE≌△CAD得
由已知条件,先证明△ABE≌△CAD得![]() ,可得
,可得![]() .即可求出
.即可求出![]() 的长.
的长.
试题解析:
![]() AE=CD,AC=BC,
AE=CD,AC=BC,
∴EC=BD;
∵△ABC为等边三角形,
![]()
在△BEC与△ADB中,
∴△BEC≌△ADB(SAS),
∴∠EBC=∠BAD;
∵∠ABE+∠EBC=![]() ,则∠ABE+∠BAD=
,则∠ABE+∠BAD=![]() ,
,
∵∠BPQ是△ABP外角,
∴∠ABP+∠BAP=![]() =∠BPQ,
=∠BPQ,
又∵BQ⊥AD,
![]()
∴BP=2PQ.
![]() ∵△ABC为等边三角形,
∵△ABC为等边三角形,
∴AB=CA,∠BAE=∠ACD=![]() ;
;
又∵AE=CD,
在△ABE和△CAD中,
∴△ABE≌△CAD(SAS);
∴BE=AD,∠CAD=∠ABE;
![]()
∵BQ⊥AD,
![]() ,则
,则![]()
∵PQ=3,
∴在Rt△BPQ中,BP=2PQ=6;
又∵PE=1,
∴AD=BE=BP+PE=7.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校为了做好大课间活动,计划用400元购买10件体育用品,备选体育用品及单价如下表(单位:元)
备用体育用品 | 篮球 | 排球 | 羽毛球拍 |
单位(元) | 50 | 40 | 25 |
(1)若400元全部用来购买篮球和羽毛球拍共10件,问篮球和羽毛球拍各购买多少件?
(2)若400元全部用来购买篮球、排球和羽毛球拍三种共10件,能实现吗?若能,求出篮球、排球、羽毛球拍各购买多少件;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 分别是
分别是![]() 的中点,若等腰
的中点,若等腰![]() 绕点
绕点![]() 逆时针旋转,得到等腰
逆时针旋转,得到等腰![]() ,设旋转角为
,设旋转角为![]() ,记直线
,记直线![]() 与
与![]() 的交点为
的交点为![]()


(1)如图![]() ,当
,当![]() 时,线段
时,线段![]() 的长等于 ,线段
的长等于 ,线段![]() 的长等于 .(直接填写结果)
的长等于 .(直接填写结果)
(2)如图![]() ,当
,当![]() 时,求证:
时,求证:![]() ,且
,且![]() ;
;
(3)设![]() 的中点为
的中点为![]() ,则线段
,则线段![]() 的长为 (直接填写结果).
的长为 (直接填写结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市建设森林城市需要大量的树苗,某生态示范园负责对甲、乙、丙、丁四个品种的树苗共500株进行树苗成活率试验,从中选择成活率高的品种进行推广.通过试验得知:丙种树苗的成活率为89.6%,把试验数据绘制成下面两幅统计图.(部分信息未给出)
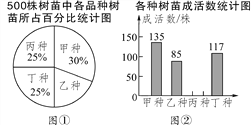
(1)试验所用的乙种树苗的数量是_______株;
(2)求出丙种树苗的成活数,并把图②补充完整;
(3)你认为应选哪种树苗进行推广?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=![]() AC,连接AE交OD于点F,连接CE、OE.
AC,连接AE交OD于点F,连接CE、OE.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
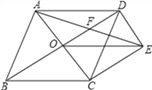
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如图正方形
中,如图正方形![]() 的顶点
的顶点![]() ,
,![]() 坐标分别为
坐标分别为![]() ,
,![]() ,点
,点![]() ,
,![]() 坐标分别为
坐标分别为![]() ,
,![]() ,且
,且![]() ,以
,以![]() 为边作正方形
为边作正方形![]() .设正方形
.设正方形![]() 与正方形
与正方形![]() 重叠部分面积为
重叠部分面积为![]() .
.

(1)①当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为______;②当点
的值为______;②当点![]() 与点
与点![]() 重合时,
重合时,![]() 的值为______.
的值为______.
(2)请用含![]() 的式子表示
的式子表示![]() ,并直接写出
,并直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学统计了家中10月份的长途电话清单,并按通话时间画出了如图所示的统计图(每组数据含左端点值,不含右端点值).
(1)该同学家这个月一共打了多少次长途电话?
(2)通话时间不足10分钟的有多少次?
(3)哪个时间范围内的通话次数最多?哪个时间范围内的通话次数最少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=![]() ,点D为AC与反比例函数
,点D为AC与反比例函数![]() 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.
的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com