
����Ŀ����a,b��������������ʵ�������ǹ涨�����㲻��ʽa��x��b��ʵ��x������ȡֵ��ȫ����������䣬��ʾΪ[a,b]������һ����������������Ա���x�뺯��ֵy���㣺��m��x��nʱ����m��y��n,���Ǿͳƴ˺����DZ�����[m.n]�ϵġ��պ��������纯�� ![]() ����x=1ʱ��y=3����x=3ʱ��y=1������
����x=1ʱ��y=3����x=3ʱ��y=1������ ![]() ʱ����
ʱ���� ![]() ������˵����
������˵���� ![]() �DZ�����[1,3]�ϵġ��պ�������
�DZ�����[1,3]�ϵġ��պ�������
��1������������y= ![]() �DZ�����[1,2016]�ϵġ��պ����������жϲ�˵�����ɣ�
�DZ�����[1,2016]�ϵġ��պ����������жϲ�˵�����ɣ�
��2�������κ���y= ![]() �DZ�����[1,2]�ϵġ��պ���������k��ֵ��
�DZ�����[1,2]�ϵġ��պ���������k��ֵ��
��3����һ�κ���y=kx+b(k��0)�DZ�����[m��n]�ϵġ��պ���������˺����ı���ʽ���ú�m��n�Ĵ���ʽ��ʾ����
���𰸡�
��1���⣺����������y= ![]() �DZ�����[1,2016]�ϵġ��պ�������
�DZ�����[1,2016]�ϵġ��պ�������
�������£�
����������y= ![]() �ڵ�һ���ޣ�y��x���������С��
�ڵ�һ���ޣ�y��x���������С��
��x=1ʱ��y=2016�� ��x=2016ʱ��y=1��
��ͼ����㣨1,2016���ͣ�2016,1��
�൱1��x��2016ʱ����1��y��2016�����ϱպ����Ķ��壬
�෴��������y= ![]() �DZ�����[1��2016]�ϵġ��պ�����
�DZ�����[1��2016]�ϵġ��պ�����
��2���⣺���ڶ��κ��� ![]() ��ͼ�����ϣ�
��ͼ�����ϣ�
�Գ���Ϊ ![]() ��
��
����κ��� ![]() �ڱ�����[1,2]�ڣ�y��x�����������
�ڱ�����[1,2]�ڣ�y��x�����������
��x=1ʱ��y=1��
��k= ![]() ��
��
��x=2ʱ��y=2��
��k= ![]() ��
��
��ͼ����㣨1,1���ͣ�2,2��
�൱1��x��2ʱ����1��y��2�����ϱպ����Ķ��壬
��k= ![]()
��3���⣺��Ϊһ�κ��� ![]() �DZ�����
�DZ����� ![]() �ϵġ��պ�������
�ϵġ��պ�������
����һ�κ�����ͼ�������ʣ��У�
���� ![]() ʱ����ͼ����㣨m,m���ͣ�n,n��
ʱ����ͼ����㣨m,m���ͣ�n,n��
![]() ��
��
��� ![]() ��
��
�� ![]()
���� ![]() ʱ����ͼ����㣨m,n���ͣ�n,m��
ʱ����ͼ����㣨m,n���ͣ�n,m��
![]() �����
����� ![]()
�� ![]() ��
��
��һ�κ����ı���ʽΪ ![]() ��
�� ![]()
����������1�����ݷ���������y=![]() �ڵ�һ���ޣ�y��x���������С����x=1ʱ��y=2016����x=2016ʱ��y=1����ͼ����㣨1��2016���ͣ�2016��1������1��x��2016ʱ����1��y��2016�����ϱպ����Ķ��壬�õ�����������y=
�ڵ�һ���ޣ�y��x���������С����x=1ʱ��y=2016����x=2016ʱ��y=1����ͼ����㣨1��2016���ͣ�2016��1������1��x��2016ʱ����1��y��2016�����ϱպ����Ķ��壬�õ�����������y=![]() �DZ�����[1��2016]�ϵġ��պ���������2�����ڶ��κ��� y=x22xk��ͼ�����ϣ��Գ���Ϊ
�DZ�����[1��2016]�ϵġ��պ���������2�����ڶ��κ��� y=x22xk��ͼ�����ϣ��Գ���Ϊ![]() �����κ���
�����κ���![]() �ڱ�����[1��2]�ڣ�y��x�����������x=1ʱ��y=1��k=
�ڱ�����[1��2]�ڣ�y��x�����������x=1ʱ��y=1��k= ![]() ����x=2ʱ��y=2��k=
����x=2ʱ��y=2��k= ![]() ����ͼ����㣨1��1���ͣ�2��2����1��x��2ʱ����1��y��2�����ϱպ����Ķ��壬���k��ֵ����3������һ�κ�����ͼ�������ʣ���k��0ʱ���õ�y=x����k��0ʱ���õ�y=-x+m+n���õ�һ�κ����ı���ʽ.
����ͼ����㣨1��1���ͣ�2��2����1��x��2ʱ����1��y��2�����ϱպ����Ķ��壬���k��ֵ����3������һ�κ�����ͼ�������ʣ���k��0ʱ���õ�y=x����k��0ʱ���õ�y=-x+m+n���õ�һ�κ����ı���ʽ.![]()


 ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABC�У���A=65������B=75��������C��DE���ۣ�ʹ��C������ABC��ĵ�![]() ��������1=20�������2�Ķ���Ϊ( )
��������1=20�������2�Ķ���Ϊ( )

A. 80��B. 90��
C. 100��D. 110��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���ֱ�ߺ�Բ������BAD��ƽ����AG��BC�ڵ�E����BF=12��AB=10����AE�ij�Ϊ�� ��

A��16 B��15 C��14 D��13
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������y=x2+bx+c�����㣨2��-3���ͣ�4��5��.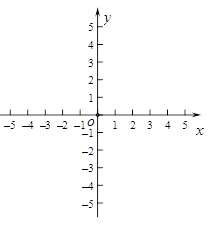
��1���������ߵı���ʽ���������ꣻ
��2������������x�ᷭ�ۣ��õ�ͼ��G����ͼ��G�ı���ʽ��
��3���ڣ�2���������£���-2<x<2ʱ��ֱ��y=m���ͼ����һ�������㣬��m��ֵ��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB��CD������ͼ�й��ɼ�����ȥ�����1����2��������n����(����)
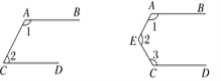

A. n��180�� B. 2n��180�� C. (n��1)��180�� D. (n��1)2��180��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y= ![]() ��y�ύ�ڵ�A����ֱ��y=��
��y�ύ�ڵ�A����ֱ��y=�� ![]() ���ڵ�B����ABΪ������������ABCD����Cǡ��ԭ��O�غϣ�������y=��x��h��2+k�Ķ�����ֱ��y=��
���ڵ�B����ABΪ������������ABCD����Cǡ��ԭ��O�غϣ�������y=��x��h��2+k�Ķ�����ֱ��y=�� ![]() ���ƶ����������������εı�AB��BC���й����㣬��h��ȡֵ��Χ�ǣ� ��
���ƶ����������������εı�AB��BC���й����㣬��h��ȡֵ��Χ�ǣ� ��
A.��2 ![]()
B.��2��h��1
C.��1 ![]()
D.��1 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У�M��N��BD�����ȷֵ㣬����CM���ӳ���AB�ڵ�E������EN���ӳ���CD�ڵ�F�����½��ۣ�
��EΪAB���е㣻
��FC=4DF��
��S��ECF= ![]() ��
��
�ܵ�CE��BDʱ����DFN�ǵ��������Σ�
����һ����ȷ���� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����ͬ�����ݵij˷�����Ϊ��am��an��am��n(����a��0��m��nΪ������)�����Ƶ����ǹ涨��������������m��n��һ�������㣺h(m��n)��h(m)��h(n)�������������������գ�
(1)��h(1)��![]() ����h(2)��________��
����h(2)��________��
(2)��h(1)��k(k��0)����h(n)��h(2017)��________(�ú�n��k�Ĵ���ʽ��ʾ������nΪ������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A=2x2+3xy��2x��1��B=��x2+xy��1��
��1����3A+6B��
��2����3A+6B��ֵ��x�أ���y��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com