

���� ��1�����õȽǶԵȱ�֤��AB=BE=AF���õ�BE��BE����BE=BE�������ı���ABEF��ƽ���ı��Σ�������һ���ڱ���ȵ�ƽ���ı��������ο�֤��
��2������AC��C��F����֤��AEC�ա�C��EF���ɵ�AC=FC'��
��3����֤A��E��C��������ͬһֱ���ϣ���֪�ı���ABEF�����Σ����ԡ�EPC��=90�㣬�����PF��PE��EC��ij������ù��ɶ������C��F���ɣ�
��� �⣺��1����ͼ1��
���ı���ABCD��ƽ���ı��Σ�
��AD��BC��
���1=��5
�ߡ�1=��2��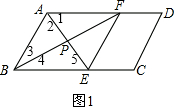
���2=��5
��AB=BE��
ͬ����AB=AF��
��AF=BE
�֡�AF��BE��
���ı���ABEF��ƽ���ı��Σ�
�֡�AB=AF��
���ı���ABEF�����Σ�
��2����ͼ2������CA��C'F��
�ߡ�ABC=60�㣬�ı���ABEF�����Σ�
���AEB=��AEF=��FEC=��F'EC'=60�㣬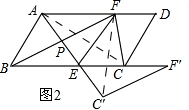
���AEC=��FEC'=120
�ڡ�AEC�͡�FEC'
$\left\{\begin{array}{l}{AE=FE}\\{��AEC=��FEC'}\\{EC=EC'}\end{array}\right.$
���AEC�ա�FEC'��
��AC=FC'��
��3����ͼ2���ɡ�F'EC'=60�㣬��AEC=��FEC��=120�㣬��֪��A��E��C������ͬһ��ֱ���ϣ�
�ߡ�ABC=60�㣬�ı���ABEF�����Σ�
��BF��AE��PF=BP����ABE�ǵȱ������Σ�
��PE=$\frac{1}{2}$BE=3��PF=BP=BE•cos30��=3$\sqrt{3}$��
��EC'=EC=8-6=2��
����Rt��C'PF��C��F=$\sqrt{P{F}^{2}+PC{��}^{2}}$=$\sqrt{��3\sqrt{3��^{2}+{5}^{2}}}$=2$\sqrt{13}$��
���� ������Ҫ������ƽ���ı��ε����ʣ����ε��ж����ʣ������ε�ȫ���ж������ʣ����ɶ������ܹ�����ת�任�й����ȫ���κ�ֱ���������ǽ������Ĺؼ���


 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
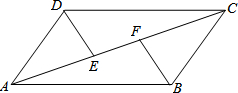 ��֪����ͼE��F��?ABCD�ĶԽ���AC�ϵ����㣬��AF=CE����֤��DE=BF��
��֪����ͼE��F��?ABCD�ĶԽ���AC�ϵ����㣬��AF=CE����֤��DE=BF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
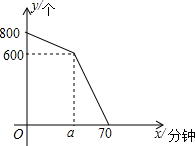 �ڸ�Ů��ǰ��ij�����վ�Ŀ�������������ӣ�ÿ����ݵ�����վ����Ҫ���п�ݵ��ŵ�ɨ�裬��Ů�ڵ�������ϣ������վ�ڽ��п�ݵ���ɨ��ǰ�����յ�800��δɨ���ݣ���ɨ�����ʼ��������ƽ��ÿ������10��δɨ���ݵ�������վ��ɨ���ƽ��ÿ����ɨ��15����ݵ��ţ���֪��ɨ�����ʼ����a������ֻ��һ̨ɨ����������ڸ�Ů�ڵ���δɨ��Ŀ�ݸ���y��������ɨ�������ʱ��x�����ӣ�֮��Ĺ�ϵ��ͼ��ʾ��
�ڸ�Ů��ǰ��ij�����վ�Ŀ�������������ӣ�ÿ����ݵ�����վ����Ҫ���п�ݵ��ŵ�ɨ�裬��Ů�ڵ�������ϣ������վ�ڽ��п�ݵ���ɨ��ǰ�����յ�800��δɨ���ݣ���ɨ�����ʼ��������ƽ��ÿ������10��δɨ���ݵ�������վ��ɨ���ƽ��ÿ����ɨ��15����ݵ��ţ���֪��ɨ�����ʼ����a������ֻ��һ̨ɨ����������ڸ�Ů�ڵ���δɨ��Ŀ�ݸ���y��������ɨ�������ʱ��x�����ӣ�֮��Ĺ�ϵ��ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ABC=90�㣬��D�ڱ�AC�ϣ��߶�DB�Ƶ�D˳ʱ����ת���˵�Bǡ�����ڱ�AB�ϵĵ�E�������$\frac{AE}{EB}$=y��$\frac{AD}{DC}$=x����ôy��x����Ĺ�ϵʽ�ǣ�y=$\frac{x-1}{2}$���ú�x�Ĵ���ʽ��ʾy����
��ͼ����Rt��ABC�У���ABC=90�㣬��D�ڱ�AC�ϣ��߶�DB�Ƶ�D˳ʱ����ת���˵�Bǡ�����ڱ�AB�ϵĵ�E�������$\frac{AE}{EB}$=y��$\frac{AD}{DC}$=x����ôy��x����Ĺ�ϵʽ�ǣ�y=$\frac{x-1}{2}$���ú�x�Ĵ���ʽ��ʾy�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��E��F�ֱ��DZ�AB��AC�е㣬D��BC����һ�㣬����AED=��AFD�������ı���AEDF��ƽ���ı�����Ϊʲô��
��ͼ��E��F�ֱ��DZ�AB��AC�е㣬D��BC����һ�㣬����AED=��AFD�������ı���AEDF��ƽ���ı�����Ϊʲô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
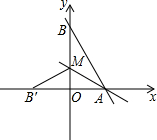 ��ͼ��ֱ��y=-$\frac{4}{3}$x+8��x�ᣬy��ֱ��ڵ�A��B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B�䴦�����AMO�����Ϊ9��
��ͼ��ֱ��y=-$\frac{4}{3}$x+8��x�ᣬy��ֱ��ڵ�A��B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B�䴦�����AMO�����Ϊ9���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com