
【题目】如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F. 
(1)求证:四边形ABCD是正方形;
(2)当AE=2EF时,判断FG与EF有何数量关系?并证明你的结论.
【答案】
(1)证明:∵∠CED是△BCE的外角,∠AED是△ABE的外角,
∴∠CED=∠CBE+∠BCE,∠AED=∠BAE+∠ABE,
∵∠BAE=∠BCE,∠AED=∠CED,
∴∠CBE=∠ABE,
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=∠BAD=90°,AB=CD,
∴∠CBE=∠ABE=45°,
∴△ABD与△BCD是等腰直角三角形,
∴AB=AD=BC=CD,
∴四边形ABCD是正方形
(2)解:当AE=2EF时,FG=3EF.
证明:∵四边形ABCD是正方形,
∴AB∥CD,AD∥BC,
∴△ABE∽△FDE,△ADE∽△GBE,
∵AE=2EF,
∴BE:DE=AE:EF=2,
∴BG:AD=BE:DE=2,
即BG=2AD,
∵BC=AD,
∴CG=AD,
∵△ADF∽△GCF,
∴FG:AF=CG:AD,
即FG=AF=AE+EF=3EF
【解析】(1)由∠BAE=∠BCE,∠AED=∠CED,利用三角形外角的性质,即可得∠CBE=∠ABE,又由四边形ABCD是矩形,即可证得△ABD与△BCD是等腰直角三角形,继而证得四边形ABCD是正方形;(2)由题意易证得△ABE∽△FDE,△ADE∽△GBE,△ADF∽△GCF,由AE=2EF,利用相似三角形的对应边成比例,即可求得FG=3EF.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对正方形的判定方法的理解,了解先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】根据不等式的基本性质,把下列不等式化成“x>a”或“x<a”的形式:
(1)4x>3x+5 (2)-2x<17
(3)0.3x<-0.9 (4)x<![]() x-4
x-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
造型花卉 | 甲 | 乙 |
A | 80 | 40 |
B | 50 | 70 |
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由※组成的图案和算式,解答问题:

1+3=22=4
1+3+5=32=9
1+3+5+7=42=16
1+3+5+7+9=52=25
(1)猜想1+3+5+7+9+…+29= = ;
(2)猜想1+3+5+7+9+…+(2n﹣1)+(2n+1)= = ;
(3)用上述规律计算:41+43+45+…+77+79.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦进货员在苏州发现了一种应季围巾,用8000元购进一批围巾后,发现市场还有较大的需求,又在上海用17600元购进了同一种围巾,数量恰好是在苏州所购数量的2倍,但每条比在苏州购进的多了4元.问某商厦在苏州、上海分别购买了多少条围巾?
查看答案和解析>>
科目:初中数学 来源: 题型:
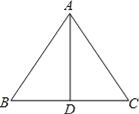
【题目】如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__.
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解答下列各题:
(1)解不等式:3x-5<2(2+3x);
(2)解不等式:2x-3≤![]() (x+2);
(x+2);
(3)解不等式: ![]() <x-1,并将解集在数轴上表示出来.
<x-1,并将解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB。
![]()
(1)用尺规作图的方法作出线段AB的垂直平分线l(保留作图痕迹,不要求写出作法);
(2)在(1)中所作的直线l上任意取两点M、N(线段AB的上方),连接AM、AN。BM、BN。
求证:∠MAN=∠MBN。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com