
分析 (1)点P、点A代入即可求出抛物线解析式;
(2)可以根据已知画出二次函数图象,根据图象分析可以证明m>0.
(3)利用二次函数交点式与一般式写出等式,根据特殊点带入,求出cm的一个代数式,通过展开代数式和代数式因式分解,即可证明m<1.
解答 解:(1)由二次函数y=x2+bx+c的图象经过点P(2,$\frac{1}{2}$)和点A(1,0),
可得$\left\{\begin{array}{l}{4+2b+c=\frac{1}{2}}\\{1+b+c=0}\end{array}\right.$,解得到$\left\{\begin{array}{l}{b=-\frac{5}{2}}\\{c=\frac{3}{2}}\end{array}\right.$,
∴抛物线解析式为y=x2-$\frac{5}{2}$x+$\frac{3}{2}$,
(2)∵二次函数y=x2+ax+b二次项系数为1,
∴二次函数图象抛物线开口向上.
∵二次函数y=x2+ax+b的图象经过点P(2,m),与x轴交于A(p,0),B(q,0),且0<p<q<2,如图: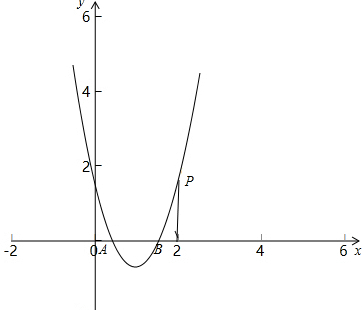
∴二次函数当x=q时,y=0,且x>q时,y随x的增大而增大,
∴m>0;
(3)由已知得:x2+ax+b=(x-p)(x-q),
令x=0得c=pq,
令x=2得m=(2-p)(2-q),
∴cm=pq(2-p)(2-q)=[1-(x-p)2][1-(q-1)2],
∵0<p<q<2,
0<1-(x-p)2<1,0<1-(q-1)2<1,
并且1-(x-p)2=1和1-(q-1)2=1不能同时成立,
∴0<cm<1,
又∵c≥1,
∴m<1.
点评 考查了待定系数法求二次函数的经销商以及二次函数图象与坐标轴交点知识,同时考查学生分析问题解决问题能力,特别是代数式的变形,更能看出本题作为奥数解答题的重要性.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
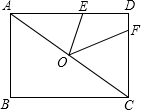 如图,矩形ABCD中,点O为AC的中点,E,F分别在AD,CD上,且AE=AO,CF=CO.
如图,矩形ABCD中,点O为AC的中点,E,F分别在AD,CD上,且AE=AO,CF=CO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com