
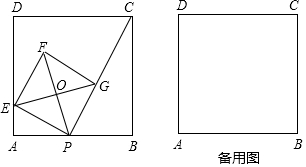
���� ��1���������ε����ʵó���A=��B=��EPG=90�㣬PF��EG��AB=BC=4����OEP=45�㣬�ɽǵĻ����ϵ֤����AEP=��BPC���ó���APE�ס�BCP���ó���Ӧ�߳ɱ����������AE�ij���
��2����A��P��O��E�ĵ㹲Բ�����ɵó����ۣ�
������OA��AC���ɹ��ɶ������AC=4$\sqrt{2}$����Բ�ܽǶ����ó���OAP=��OEP=45�㣬�ܳ���O��AC�ϣ���P�˶�����Bʱ��OΪAC���е㣬���ɵó��𰸣�
��3�����APE�����Բ��Բ��ΪM����MN��AB��N������������λ�߶����ó�MN=$\frac{1}{2}$AE����AP=x����BP=4-x�������������εĶ�Ӧ�߳ɱ������AE=x-$\frac{1}{4}$x2=-$\frac{1}{4}$��x-2��2+1���ɶ��κ��������ֵ���AE�����ֵΪ1���ó�MN�����ֵ=$\frac{1}{2}$���ɣ�
��� ��1���⣺���ı���ABCD���ı���PEFG�������Σ�
���A=��B=��EPG=90�㣬PF��EG��AB=BC=4����OEP=45�㣬
���AEP+��APE=90�㣬��BPC+��APE=90�㣬
���AEP=��BPC��
���APE�ס�BCP��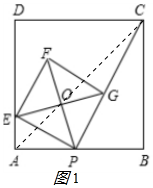
��$\frac{AE}{BP}=\frac{AP}{BC}$����$\frac{AE}{4-1}=\frac{1}{4}$��
��ã�AE=$\frac{3}{4}$��
�ʴ�Ϊ��$\frac{3}{4}$��
��2����֤������PF��EG��
���EOP=90�㣬
���EOP+��A=180�㣬
��A��P��O��E�ĵ㹲Բ��
���Oһ���ڡ�APE�����Բ�ϣ�
�ڽ⣺����OA��AC����ͼ1��ʾ��
���ı���ABCD�������Σ�
���B=90�㣬��BAC=45�㣬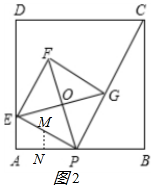
��AC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$��
��A��P��O��E�ĵ㹲Բ��
���OAP=��OEP=45�㣬
���O��AC�ϣ�
��P�˶�����Bʱ��OΪAC���е㣬OA=$\frac{1}{2}$AC=2$\sqrt{2}$��
����O������·����Ϊ2$\sqrt{2}$��
��3���⣺���APE�����Բ��Բ��ΪM����MN��AB��N����ͼ2��ʾ��
��MN��AE��
��ME=MP��
��AN=PN��
��MN=$\frac{1}{2}$AE��
��AP=x����BP=4-x��
�ɣ�1���ã���APE�ס�BCP��
��$\frac{AE}{BP}=\frac{AP}{BC}$����$\frac{AE}{4-x}=\frac{x}{4}$��
��ã�AE=x-$\frac{1}{4}$x2=-$\frac{1}{4}$��x-2��2+1��
��x=2ʱ��AE�����ֵΪ1����ʱMN��ֵ���=$\frac{1}{2}$��1=$\frac{1}{2}$��
����APE��Բ�ĵ�AB�ߵľ�������ֵΪ$\frac{1}{2}$��
���� ������Բ���ۺ���Ŀ�������������ε����ʡ��ĵ㹲Բ��Բ�ܽǶ����������ε����Բ�����������ε��ж������ʡ����ɶ��������κ�������ֵ��֪ʶ�������ۺ���ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
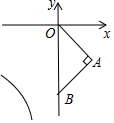 ��ͼ��ƽ��ֱ������ϵ�У�����Rt��OAB��x�Ḻ��������ƽ�ƺ�õ���O1A1B1��ʹ��B�Ķ�Ӧ��B1����˫����y=$\frac{8}{x}$��x��0���ϣ�����B��0��-4�������߶�ABɨ��������ǣ�ƽ����λ����������
��ͼ��ƽ��ֱ������ϵ�У�����Rt��OAB��x�Ḻ��������ƽ�ƺ�õ���O1A1B1��ʹ��B�Ķ�Ӧ��B1����˫����y=$\frac{8}{x}$��x��0���ϣ�����B��0��-4�������߶�ABɨ��������ǣ�ƽ����λ����������| A�� | 2 | B�� | 2$\sqrt{2}$ | C�� | 4 | D�� | 4$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
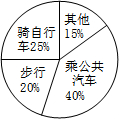 ijУѧ����У��ʽ�����ͳ��ͼ��ͼ��ʾ������У���е�У��ѧ����100�ˣ���˹���������У��ѧ���У�������
ijУѧ����У��ʽ�����ͳ��ͼ��ͼ��ʾ������У���е�У��ѧ����100�ˣ���˹���������У��ѧ���У�������| A�� | 75�� | B�� | 100�� | C�� | 125�� | D�� | 200�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
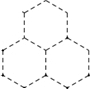 ��ͼ�����ɴ�С��ȫ��ͬ������������ɵ�ͼ�Σ�С�����ú�ɫ����ɫ����ɫ�����ÿ���������ηֱ�Ϳ�����е�һ����ɫ�����Ϸ�����������Ϳ��ɫ�ĸ�����$\frac{1}{3}$��
��ͼ�����ɴ�С��ȫ��ͬ������������ɵ�ͼ�Σ�С�����ú�ɫ����ɫ����ɫ�����ÿ���������ηֱ�Ϳ�����е�һ����ɫ�����Ϸ�����������Ϳ��ɫ�ĸ�����$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
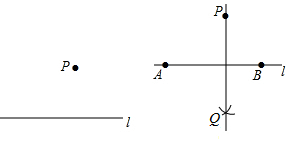
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com